
����Ŀ����ͼ����ABC�ǵȱ������Σ�AB=2cm������P��Q�ֱ�ӵ�A��Cͬʱ�������˶��ٶȾ�Ϊ1cm/s����P�ӵ�A��������A��B�˶�������Bֹͣ����Q�ӵ�C��������C��A�˶�������Aֹͣ������BQ��CP�ཻ�ڵ�D�����P���˶�ʱ��Ϊx��s����
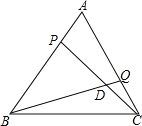
��1��AP= ���ú�x��ʽ�ӱ�ʾ����
��2����֤����ACP�ա�CBQ��
��3������PDB�Ķ�����
��4����CP��ABʱ��ֱ��д��x��ֵ��
���𰸡���1��x����2����������3����PDB=60������4��x=1��
��������
�����������1�����ݵ�P���˶�ʱ��Ϊx��s�����˶��ٶȾ�Ϊ1cm/s���õ�AP=x��
��2������SAS֤����ACP�ա�CBQ��
��3������ACP�ա�CBQ���õ���ACP=��QCB��������ǵ�������PDB=��DBC+��DCB�����ɽ��
��4����CP��ABʱ�����PΪAB���е㣬����AP=![]() AB=1cm����x=1��
AB=1cm����x=1��
�⣺��1������P���˶�ʱ��Ϊx��s�����˶��ٶȾ�Ϊ1cm/s��
��AP=x��
�ʴ�Ϊ��x��
��2��������P��Q�ֱ�ӵ�A��Cͬʱ�������˶��ٶȾ�Ϊ1cm/s����P�ӵ�A��������A��B�˶�������Bֹͣ����Q�ӵ�C��������C��A�˶�������Aֹͣ��
��AP=CQ��
�ߡ�ABC�ǵȱ������Σ�
��AC=CB����A=��ACB=60����
����ACP����CBQ��
 ��
��
���ACP�ա�CBQ��
��3���ߡ�ACP�ա�CBQ��
���ACP=��QCB��
�ߡ�PDB=��DBC+��DCB��
���PDB=��DCB+��ACP=��ACB=60����
��4����CP��ABʱ�����PΪAB���е㣬
��AP=![]() AB=1cm��
AB=1cm��
��x=1��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
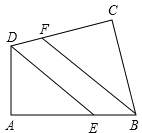
����Ŀ����ͼ���ı���ABCD�У���A=��C=90�㣬BF��DE�ֱ�ƽ�֡�ABC����ADC���ж�DE��BF�Ƿ�ƽ�У���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ���ı���ABCD���ܳ���18��������ABC���ܳ���14����Խ���AC�ij���_____________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͨ�����������ϣ����Կ���һЩ��������Ĺ��ɣ�������2015��9�·ݵ������ƣ�
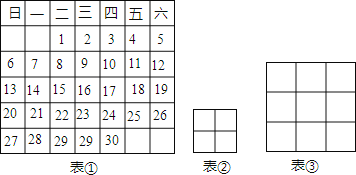
��1���ڱ����У�����ѡ�������������2��2�������ο�����Ȧ��2��2�������������߽�����ˣ���������磺�������ο�Ȧ��4��5��11��12�ĸ�����Ȼ�����ǽ�����ˣ����������4��12��5��11=��7��5��11��4��12=7�������ñ����������ο�����Ȧ��2��2�������������Ƚ�����ˣ���������г���ʽ����������ѡ������һ����ʽ���ɣ���
��2�����ñ����������ο�����Ȧ��2��2�����У��������Ƚ�����ˣ���������������Ͻǵ�����Ϊn���ú�n��ʽ�ӱ�ʾ��������λ�õ����֣��г���ʽ����������ѡ������һ����ʽ���ɣ���
��3����ѡ�������������3��3�������η�������Ȧ��3��3�������������η����ĸ���λ���ϵ�4�����Ƚ�����ˣ���������㷢����ʲô����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������и�����Ϊ���ߵ��������в���ֱ�������ε���
A. 9��12��15 B. 41��40��9 C. 25��7��24 D. 6��5��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB=AD����ô��������һ�������������ж���ABC�ա�ADC���ǣ� ��
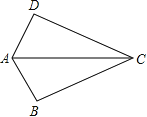
A��CB=CD B����BAC=��DAC C����BCA=��DCA D����B=��D=90��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com