
【题目】在通常的日历牌上,可以看到一些数所满足的规律,表①是2015年9月份的日历牌.
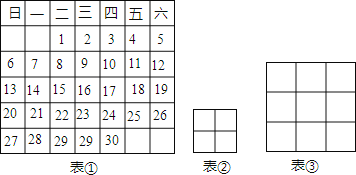
(1)在表①中,我们选择用如表②那样2×2的正方形框任意圈出2×2个数,将它们线交叉相乘,再相减,如:用正方形框圈出4、5、11、12四个数,然后将它们交叉相乘,再相减,即4×12﹣5×11=﹣7或5×11﹣4×12=7,请你用表②的正方形框任意圈出2×2个数,将它们先交叉相乘,再相减.列出算式并算出结果(选择其中一个算式即可);
(2)在用表②的正方形框任意圈出2×2个数中,将它们先交叉相乘,再相减,若设左上角的数字为n,用含n的式子表示其他三个位置的数字,列出算式并算出结果(选择其中一个算式即可);
(3)若选择用如表③那样3×3的正方形方框任意圈出3×3个数,将正方形方框四个角位置上的4个数先交叉相乘,再相减,你发现了什么?请说明理由.
【答案】(1)1×9﹣2×8=﹣7;
(2)﹣7;
(3)发现:它们最后的结果是28或﹣28,理由见解析;结论:它们的结果与n的取值无关,最终结果保持不变,是28或﹣28.
【解析】
试题分析:(1)先画出各个数,再求出即可;
(2)表示出其余的数,列出算式,求出即可;
(3)圈出各个数,列出算式,求出即可;设左上角的数为m,则其它三个位置的数分别为n+14,n+2,n+16,列出算式,求出即可.
解:(1)如图所示:
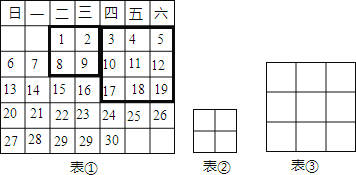
1×9﹣2×8=﹣7;
(2)其它三个数为n+1,n+7,n+8,
n(n+8)﹣(n+1)(n+7)
=n2+8n﹣n2﹣8n﹣7
=﹣7;
(3)3×19﹣5×17=﹣28,
5×17﹣3×19=28,
发现:它们最后的结果是28或﹣28,
理由是:设左上角的数为m,则其它三个位置的数分别为n+14,n+2,n+16,
则n(m+16)﹣(n+14)(n+2)
=n2+16n﹣n2﹣16n﹣28
=﹣28;
(n+14)(n+2)﹣n(n+16)
=28;
结论:它们的结果与n的取值无关,最终结果保持不变,是28或﹣28.


科目:初中数学 来源: 题型:
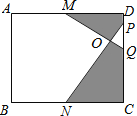
【题目】如图,在矩形ABCD中,M、N分别是边AD、BC的中点,点P、Q在DC边上,且PQ=![]() DC.若AB=16,BC=20,则图中阴影部分的面积是 .
DC.若AB=16,BC=20,则图中阴影部分的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个四边形的三个内角的度数依次如下选项,其中是平行四边形的是
A. 88°,108°,88°. B. 88°,104°,108°.
C. 88°,92°,92° . D. 88°,92°,88°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题背景】
已知:l1∥l2∥l3∥l4,平行线l1与l2、l2与l3、l3与l4之间的距离分别为d1、d2、d3,且d1=d3=1,d2=2,我们把四个顶点分别在l1、l2、l3、l4这四条平行线上的四边形称为“格线四边形”.

【问题探究】
(1)如图1,正方形ABCD为“格线四边形”,则正方形ABCD的边长为 .
(2)矩形ABCD为“格线四边形”,其长:宽=2:1,求矩形ABCD的宽.
【问题拓展】
(3)如图1,EG过正方形ABCD的顶点D且垂直l1于点E,分别交l2,l4于点F,G,将∠AEG绕点A顺时针旋转30°,得到∠AE′D′(如图2),点D′在直线l3上,以AD′为边在E′D′左侧作菱形AB′C′D′,使B′C′,分别在直线l2,l4上,求菱形AB′C′D′的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AB=2cm,动点P、Q分别从点A、C同时出发,运动速度均为1cm/s,点P从点A出发,沿A→B运动,到点B停止,点Q从点C出发,沿C→A运动,到点A停止,连接BQ、CP相交于点D,设点P的运动时间为x(s).
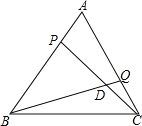
(1)AP= (用含x的式子表示);
(2)求证:△ACP≌△CBQ;
(3)求∠PDB的度数;
(4)当CP⊥AB时,直接写出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=BC,∠ABC=45°,AD是BC边上的高,E是AD上一点,ED=CD,连接EC,
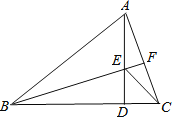
求证:
(1)△ADC≌△BDE;
(2)EA=EC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,且AE=DE.
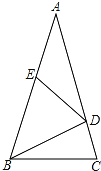
(1)写出图中三对相似比不为1的相似三角形 .
(2)选择(1)中一对加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com