
【题目】在△ABC中,AB=BC,∠ABC=45°,AD是BC边上的高,E是AD上一点,ED=CD,连接EC,
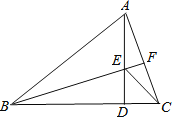
求证:
(1)△ADC≌△BDE;
(2)EA=EC.
【答案】见解析
【解析】
试题分析:(1)直接利用全等三角形的判定方法得出答案;
(2)由条件可求得∠BAC=∠BCA=67.5°,且∠BAD=∠DCE=45°,可得∠EAC=∠ECA=22.5°,可证得结论.
证明:(1)∵AD⊥BC,∠ABC=45°,
∴AD=BD,
在△ADC和△BDE中,
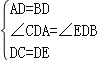 ,
,
∴△ADC≌△BDE(SAS);
(2)∵BA=BC,∠ABC=45°,
∴∠BCA=∠BAC=![]() ×135°=67.5°,
×135°=67.5°,
又∵AD⊥BC,
∴∠ADC=90°,
∵ED=CD,
∴∠ECD=45°,
∴∠ACE=67.5°﹣45°=22.5°,
∵∠AEC=∠EDC+∠ECD=135°,
∴∠EAC=180°﹣22.5°﹣135°=22.5°,
∴EA=EC.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,BC=6cm,AC=8cm,点P从点A开始沿AC向点C以2厘米/秒的速度运动;与此同时,点Q从点C开始沿CB边向点B以1厘米/秒的速度运动;如果P、Q分别从A、C同时出发,当其中一点到达终点时,另一点也随之停止运动.

(1)经过几秒,△CPQ的面积等于3cm2?
(2)在整个运动过程中,是否存在某一时刻t,使PQ恰好平分△ABC的面积?若存在,求出运动时间t;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在通常的日历牌上,可以看到一些数所满足的规律,表①是2015年9月份的日历牌.
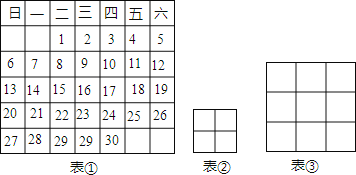
(1)在表①中,我们选择用如表②那样2×2的正方形框任意圈出2×2个数,将它们线交叉相乘,再相减,如:用正方形框圈出4、5、11、12四个数,然后将它们交叉相乘,再相减,即4×12﹣5×11=﹣7或5×11﹣4×12=7,请你用表②的正方形框任意圈出2×2个数,将它们先交叉相乘,再相减.列出算式并算出结果(选择其中一个算式即可);
(2)在用表②的正方形框任意圈出2×2个数中,将它们先交叉相乘,再相减,若设左上角的数字为n,用含n的式子表示其他三个位置的数字,列出算式并算出结果(选择其中一个算式即可);
(3)若选择用如表③那样3×3的正方形方框任意圈出3×3个数,将正方形方框四个角位置上的4个数先交叉相乘,再相减,你发现了什么?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
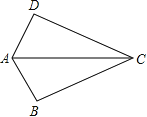
A.CB=CD B.∠BAC=∠DAC C.∠BCA=∠DCA D.∠B=∠D=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)定理是真命题(填“真”或“假”,下同).
“如果ab=0,那么a=0”是____命题.
“如果a=0,那么ab=0” 是____命题.
(2)“如果(a-1)(a-2)=0,那么a=2”是假命题,反例是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题的个数是( )
①同位角相等;②a,b,c是三条直线,若a⊥b,b⊥c,则a⊥c;③a,b,c是三条直线,若a∥b,b∥c,则a∥c;④过一点有且只有一条直线与已知直线平行.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com