
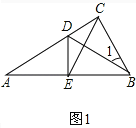
【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于点E.
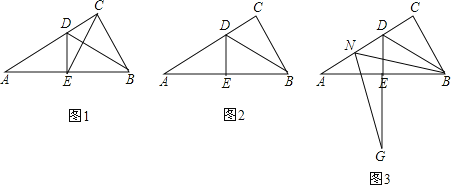
(1)如图1,连接EC,求证:△EBC是等边三角形;
(2)点M是线段CD上的一点(不与点C,D重合),以BM为一边,在BM的下方作∠BMG=60°,MG交DE延长线于点G.请你在图2中画出完整图形,并直接写出MD,DG与AD之间的数量关系;
(3)如图3,点N是线段AD上的一点,以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G.试探究ND,DG与AD数量之间的关系,并说明理由.
【答案】(1)证明见解析;(2)画图见解析,AD=DG+DM;(3)AD=DG﹣DN,理由见解析.
【解析】
试题分析:(1)利用“三边相等”的三角形是等边三角形证得△EBC是等边三角形;
(2)延长ED使得DW=DM,连接MN,即可得出△WDM是等边三角形,利用△WGM≌△DBM即可得出BD=WG=DG+DM,再利用AD=BD,即可得出答案;
(3)利用等边三角形的性质得出∠H=∠2,进而得出∠DNG=∠HNB,再求出△DNG≌△HNB即可得出答案.
(1)证明:如图1所示:
在Rt△ABC中,∠ACB=90°,∠A=30°,
∴∠ABC=60°,BC=![]() .
.
∵BD平分∠ABC,
∴∠1=∠DBA=∠A=30°.
∴DA=DB.
∵DE⊥AB于点E.
∴AE=BE=![]() .
.
∴BC=BE.
∴△EBC是等边三角形;
(2)结论:AD=DG+DM.
证明:
如图2所示:延长ED使得DW=DM,连接MW,
∵∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于点E,
∴∠ADE=∠BDE=60°,AD=BD,
又∵DM=DW,
∴△WDM是等边三角形,
∴MW=DM,
在△NGM和△DBM中,
∵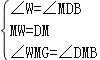
∴△WGM≌△DBM,
∴BD=WG=DG+DM,
∴AD=DG+DM.
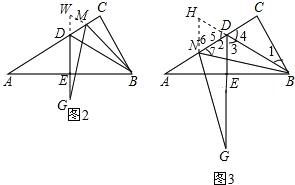
(3)结论:AD=DG﹣DN.
证明:延长BD至H,使得DH=DN.
由(1)得DA=DB,∠A=30°.
∵DE⊥AB于点E.
∴∠2=∠3=60°.
∴∠4=∠5=60°.
∴△NDH是等边三角形.
∴NH=ND,∠H=∠6=60°.
∴∠H=∠2.
∵∠BNG=60°,
∴∠BNG+∠7=∠6+∠7.
即∠DNG=∠HNB.
在△DNG和△HNB中,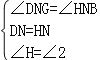
∴△DNG≌△HNB(ASA).
∴DG=HB.
∵HB=HD+DB=ND+AD,
∴DG=ND+AD.
∴AD=DG﹣ND.


科目:初中数学 来源: 题型:
【题目】某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得河的宽度,他们是这样做的:
①在河流的一条岸边B点,选对岸正对的一棵树A;
②沿河岸直走20m有一树C,继续前行20m到达D处;
③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;
④测得DE的长为5米.
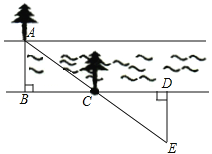
求:(1)河的宽度是多少米?
(2)请你证明他们做法的正确性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com