
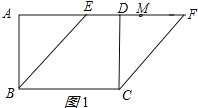
【题目】在矩形ABCD中,AD=5,AB=4,点E,F在直线AD上,且四边形BCFE为菱形.若线段EF的中点为点M,则线段AM的长为 .
【答案】5.5,或0.5
【解析】
试题分析:两种情况:①由矩形的性质得出CD=AB=4,BC=AD=5,∠ADB=∠CDF=90°,由菱形的性质得出CF=EF=BE=BC=5,由勾股定理求出DF,得出MF,即可求出AM;②同①得出AE=3,求出ME,即可得出AM的长.
解:分两种情况:①如图1所示:
∵四边形ABCD是矩形,
∴CD=AB=4,BC=AD=5,∠ADB=∠CDF=90°,
∵四边形BCFE为菱形,
∴CF=EF=BE=BC=5,
∴DF=![]() =
=![]() =3,
=3,
∴AF=AD+DF=8,
∵M是EF的中点,
∴MF=![]() EF=2.5,
EF=2.5,
∴AM=AF﹣DF=8﹣2.5=5.5;
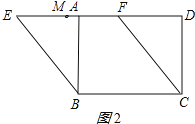
②如图2所示:同①得:AE=3,
∵M是EF的中点,
∴ME=2.5,
∴AM=AE﹣ME=0.5;
综上所述:线段AM的长为:5.5,或0.5;
故答案为:5.5,或0.5.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】下列二次函数中,图象以直线x=2为对称轴、且经过点(0,1)的是( )
A.y=(x﹣2)2+1 B.y=(x+2)2+1
C.y=(x﹣2)2﹣3 D.y=(x+2)2﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题背景】
已知:l1∥l2∥l3∥l4,平行线l1与l2、l2与l3、l3与l4之间的距离分别为d1、d2、d3,且d1=d3=1,d2=2,我们把四个顶点分别在l1、l2、l3、l4这四条平行线上的四边形称为“格线四边形”.

【问题探究】
(1)如图1,正方形ABCD为“格线四边形”,则正方形ABCD的边长为 .
(2)矩形ABCD为“格线四边形”,其长:宽=2:1,求矩形ABCD的宽.
【问题拓展】
(3)如图1,EG过正方形ABCD的顶点D且垂直l1于点E,分别交l2,l4于点F,G,将∠AEG绕点A顺时针旋转30°,得到∠AE′D′(如图2),点D′在直线l3上,以AD′为边在E′D′左侧作菱形AB′C′D′,使B′C′,分别在直线l2,l4上,求菱形AB′C′D′的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小亮、小芳和两个陌生人甲、乙同在如图所示的地下车库等电梯,已知两个陌生人到1至4层的任意一层出电梯,并设甲在a层出电梯,乙在b层出电梯.

(1)小明想求出甲、乙二人在同一层楼出电梯的概率;
(2)小亮和小芳打赌说:“若甲、乙在同一层或相邻楼层出电梯,则小亮胜,否则小芳胜”.该游戏是否公平?若公平,说明理由;若不公平,请修改游戏规则,使游戏公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于点E.
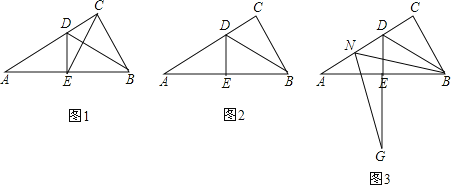
(1)如图1,连接EC,求证:△EBC是等边三角形;
(2)点M是线段CD上的一点(不与点C,D重合),以BM为一边,在BM的下方作∠BMG=60°,MG交DE延长线于点G.请你在图2中画出完整图形,并直接写出MD,DG与AD之间的数量关系;
(3)如图3,点N是线段AD上的一点,以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G.试探究ND,DG与AD数量之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算与化简:
(1)|﹣2|+(﹣2)2﹣(﹣![]() )﹣2﹣(π﹣7)0;
)﹣2﹣(π﹣7)0;
(2)[(﹣x﹣1y﹣2)﹣3﹣y(x2﹣x3y)]÷![]() x2y;
x2y;
(3)![]() ÷(﹣
÷(﹣![]() )3(﹣
)3(﹣![]() )2.
)2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:△ABC的周长为30cm,把△ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边与点E,连接AD,若AE=4cm,则△ABD的周长是( )
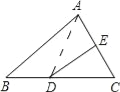
A. 22cm B. 20cm C. 18cm D. 15cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com