
【题目】中国最长铁路隧道西康铁路秦岭一线隧道全长十八点四六千米,为目前中国铁路隧道长度之首,被称为”神州第一长隧”.为了安全起见在某段隧道两旁安置了两座可旋转探照灯.如图1所示,灯A发出的光束从AC开始顺时针旋转至AD便立即回转,灯B发出的光束从BE开始顺时针旋转至BF便立即回转,两灯不停交叉照射巡视.若灯A旋转的速度是每秒3度,灯B旋转的速度是每秒2度.已知CD∥EF,且∠BAD=![]() ∠BAC,设灯A旋转的时间为t(单位:秒).
∠BAC,设灯A旋转的时间为t(单位:秒).
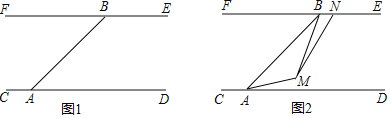
(1)求∠BAD的度数;
(2)若灯B发出的光束先旋转10秒,灯A发出的光束才开始旋转,在灯B发出的光束到达BF之前,若两灯发出的光束互相平行,求灯A旋转的时间t;
(3)如图2,若两灯同时转动,在灯A发出的光束到达AD之前,若两灯发出的光束交于点M,过点M作∠AMN交BE于点N,且∠AMN=135°.请探究:∠BAM与∠BMN的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.
【答案】(1)45;(2)当t=20秒或68秒时,两灯的光束互相平行;(3)∠BAM与∠BMN关系不会变化
【解析】
(1)因为邻补角互补,则∠BAC+∠BAD=180°,且∠BAD=![]() ∠BAC,则∠BAC:∠BAD=3:1,所以∠BAD=180°×
∠BAC,则∠BAC:∠BAD=3:1,所以∠BAD=180°×![]() =45°.(2)分情况讨论,①当0<t<60时,由平行线的性质可得∠EBE'=∠CAC',所以3t=2(10+t),求解即可;②当60<t<80时,由平行线的性质可得∠EBE'+∠C'AD=180°,所以2(10+t)+(3t-180)=180,求解即可.(3)∠BAM与∠BMN关系不会变化,利用角的和差关系分别表示出∠BAM=3t-135°,
=45°.(2)分情况讨论,①当0<t<60时,由平行线的性质可得∠EBE'=∠CAC',所以3t=2(10+t),求解即可;②当60<t<80时,由平行线的性质可得∠EBE'+∠C'AD=180°,所以2(10+t)+(3t-180)=180,求解即可.(3)∠BAM与∠BMN关系不会变化,利用角的和差关系分别表示出∠BAM=3t-135°,
∠BMN= t-45°,则∠BMN=![]() ∠BAM,所以∠BAM和∠BMN关系不会变化.
∠BAM,所以∠BAM和∠BMN关系不会变化.
解:(1)如图1,∵∠BAC+∠BAD=180°,∠BAD=![]() ∠BAC,
∠BAC,
∴∠BAC:∠BAD=3:1,
∴∠BAD=180°×![]() =45°,
=45°,
故答案为:45.
(2)设A灯转动t秒,两灯的光束互相平行,
①当0<t<60时,如图2,
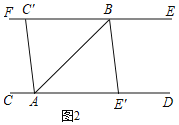
∵CD∥EF,
∴∠EBE'=∠BE'A,
∵BE'∥AC',
∴∠BE'A=∠CAC',
∴∠EBE'=∠CAC',
∴3t=2(10+t),
解得t=20.
②当60<t<80时,如图3,
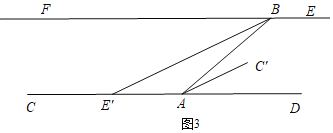
∵CD∥EF,
∴∠EBE'+∠BE'D=180°,
∵AC'∥BE',
∴∠BE'D=∠C'AD,
∴∠EBE'+∠C'AD=180°,
∴2(10+t)+(3t-180)=180,
解得t=68,
综上所述,当t=20秒或68秒时,两灯的光束互相平行.
(3)∠BAM与∠BMN关系不会变化.
.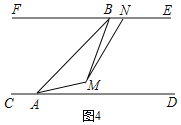
理由如下:如图4,设灯A射线转动时间为t秒,
∵∠MAD=180°-3t,
∴∠BAM=∠BAD-∠MAD=45°-(180°-3t)=3t-135°,
又∵∠ABM=∠EBA-∠EBM=135°-2t,
∴∠BMA=180°-∠ABM-∠BAM=180°-(135°-2t)-(3t-135°)=180°-t,
又∵∠AMN=135°,
∴∠BMN=∠AMN
∴∠BAM:∠BMN=3:1,
即∠BMN=![]() ∠BAM,
∠BAM,
∴∠BAM和∠BMN关系不会变化.


科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:①b2>4ac;②2a+b=0;③a+b+c>0;④若点B(-![]() ,y1),C(-
,y1),C(-![]() ,y2)为函数图象上的两点,则y1<y2.其中正确结论是___________.
,y2)为函数图象上的两点,则y1<y2.其中正确结论是___________.
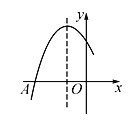
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x2-2x+3的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求点A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N,若点P在点Q左边,当矩形PMNQ的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ,过抛物线上一点F作
y轴的平行线,与直线AC交于点G(点G在点F的上方).若, ![]()
求点F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花圃销售一批名贵花卉,平均每天可售出20盆,每盆盈利40元,为了增加盈利并尽快减少库存,花圃决定采取适当的降价措施,经调查发现,如果每盆花卉每降1元,花圃平均每天可多售出2盆.
(1)若花圃平均每天要盈利1200元,每盆花卉应降价多少元?
(2)每盆花卉降低多少元时,花圃平均每天盈利最多,是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,AB∥OC,A(0,3),B(a,b),C(c,0),且a,c满足![]() .点P从点A出发,以每秒1个单位长度的速度向点B运动,点Q从点O同时出发,以每秒2个单位长度的速度向点C运动,当点Q到达点C时,点P随之停止运动.设运动时间为t(秒).
.点P从点A出发,以每秒1个单位长度的速度向点B运动,点Q从点O同时出发,以每秒2个单位长度的速度向点C运动,当点Q到达点C时,点P随之停止运动.设运动时间为t(秒).

(1)B,C两点的坐标为:B ,C ;
(2)当t为何值时,四边形PQCB是平行四边形?
(3)D为线段AB的中点,求当t为何值时,△ADQ是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红旗连锁超市准备购进甲、乙两种绿色袋装食品.甲、乙两种绿色袋装食品的进价和售价如表.已知:用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同.
甲 | 乙 | |
进价(元/袋) |
|
|
售价(元/袋) | 20 | 13 |
(1)求![]() 的值;
的值;
(2)要使购进的甲、乙两种绿色袋装食品共800袋的总利润(利润=售价-进价)不少于4800元,且不超过4900元,问该超市有几种进货方案?
(3)在(2)的条件下,该超市如果对甲种袋裝食品每袋优惠![]() 元出售,乙种袋装食品价格不变.那么该超市要获得最大利润应如何进货?
元出售,乙种袋装食品价格不变.那么该超市要获得最大利润应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,C分别在x轴,y轴上,四边形ABCO为矩形,AB=16,AC=20,点D与点A关于y轴对称,点E、F分别是线段AD、AC上的动点(点E不与点A、D重合),且∠CEF=∠ACB.
(1)直接写出BC的长是 ,点D的坐标是 ;
(2)证明:△AEF与△DCE相似;
(3)当△EFC为等腰三角形时,求点E的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com