
【题目】在![]() 中,
中,![]() 、
、![]() 相交于点
相交于点![]() 分别是
分别是![]() 中点,连接
中点,连接![]() .
.
(1)如图1,求证:四边形![]() 是平行四边形;
是平行四边形;
(2)如图2,若![]() ,求证:四边形
,求证:四边形![]() 是矩形.
是矩形.
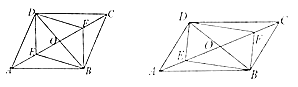
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】在日常生活中如取款、上网等都需要密码,有一种用“因式分解法”产生的密码,方便记忆,原理是对于多项![]() ,因式分解的结果是
,因式分解的结果是![]() ,若取
,若取![]() ,
,![]() 时,则各个因式的值是:
时,则各个因式的值是:![]() ,
,![]() ,
,![]() ,于是就可以把“180162”作为一个六位数的密码,对于多项式
,于是就可以把“180162”作为一个六位数的密码,对于多项式![]() ,取
,取![]() ,
,![]() 时,用上述方法产生的密码是________ (写出一个即可).
时,用上述方法产生的密码是________ (写出一个即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
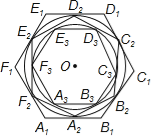
【题目】如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个正方形的边长都为1的正方形网格中,点![]() 都在格点上,从这四个点中任取三个点构成三角形,则构成的三角形中,不是直角三角形的是( )
都在格点上,从这四个点中任取三个点构成三角形,则构成的三角形中,不是直角三角形的是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
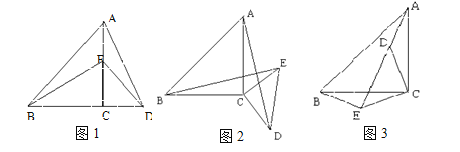
【题目】如图1,E是等腰Rt△ABC边AC上的一个动点(点E与A、C不重合),以CE为一边在Rt△ABC作等腰Rt△CDE,连结AD,BE.我们探究下列图中线段AD,、线段BE 的长度关系及所在直线的位置关系:
(1)①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系;
②将图1中的等腰Rt△CDE绕着点C按顺时针方向旋转任意角度![]() ,得到如图2、如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断.
,得到如图2、如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断.
(2)将原题中等腰直角三角形改为直角三角形(如图4—6),且AC=a,BC=b,CD=ka,CE=kb (a![]() b,k
b,k![]() 0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由.
0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由.
(3)在第(2)题图5中,连结BD、AE,且a=4,b=3,k=![]() ,求BD2+AE2的值.
,求BD2+AE2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到![]() 的位置,
的位置,![]() ,
,![]() ,平移距离为6,则阴影部分面积为
,平移距离为6,则阴影部分面积为![]()
![]()

A. 24 B. 40 C. 42 D. 48
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1+∠2=180°,∠3=∠B,求证:EF∥BC,请你补充完成下面的推导过程.
证明:∵∠1+∠2=180°(已知)
∠2=∠4( )
∴∠ +∠4=180°(等量代换)
∴DF∥AB( )
∴∠B=∠FDH( )
∵∠3=∠B( )
∴∠3=∠ ( )
∴EF∥BC( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,方格图中每个小正方形的边长为1,点A、B、C都是格点.
(1)画出△ABC关于直线MN对称的△A1B1C1;
(2)直接写出AA1的长度;
(3)如图2,A、C是直线MN同侧固定的点,D是直线MN上的一个动点,在直线MN上画出点D,使AD+DC最小.(保留作图痕迹)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国最长铁路隧道西康铁路秦岭一线隧道全长十八点四六千米,为目前中国铁路隧道长度之首,被称为”神州第一长隧”.为了安全起见在某段隧道两旁安置了两座可旋转探照灯.如图1所示,灯A发出的光束从AC开始顺时针旋转至AD便立即回转,灯B发出的光束从BE开始顺时针旋转至BF便立即回转,两灯不停交叉照射巡视.若灯A旋转的速度是每秒3度,灯B旋转的速度是每秒2度.已知CD∥EF,且∠BAD=![]() ∠BAC,设灯A旋转的时间为t(单位:秒).
∠BAC,设灯A旋转的时间为t(单位:秒).
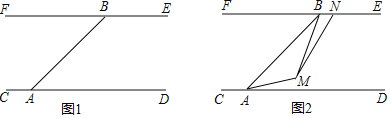
(1)求∠BAD的度数;
(2)若灯B发出的光束先旋转10秒,灯A发出的光束才开始旋转,在灯B发出的光束到达BF之前,若两灯发出的光束互相平行,求灯A旋转的时间t;
(3)如图2,若两灯同时转动,在灯A发出的光束到达AD之前,若两灯发出的光束交于点M,过点M作∠AMN交BE于点N,且∠AMN=135°.请探究:∠BAM与∠BMN的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com