
����Ŀ����һ���߳�Ϊm+3�������Σ��Ƚ�������������ڱ߳��ֱ�����1�ͼ���1���õ��ij������������ΪS1.
��1����̽���������ε����S��S1�IJ��Ƿ���һ������������ǣ�������������������ǣ�˵�����ɣ�
��2���ٽ�������������ڱ߳��ֱ�����4�ͼ���2���õ��ij������������ΪS2.
���ԱȽ�S1��S2�Ĵ�С��
����mΪ������ʱ����ij��ͼ�ε��������S1��S2֮�䣨������S1��S2�������Ϊ����������������ֵ����ֻ��16������m��ֵ��
���𰸡���1���⣺S��S1�IJ�����һ��������S��S1�IJ���1;��2������-2m+1��0����-1��m��![]() ʱ��
ʱ��![]() ��
��![]() ����-2m+1��0����m��
����-2m+1��0����m��![]() ʱ��
ʱ��![]() ��
��![]() ����-2m+1= 0����m =
����-2m+1= 0����m =![]() ʱ��
ʱ��![]() =
= ![]() ����m= 9��
����m= 9��
��������
��1��������ȫƽ����ʽ�Ͷ���ʽ���Զ���ʽ�����㼴�ɵõ���.
��2�����ȼ���S1��S2������![]() ���ٷ�������ۣ����ɵõ���.
���ٷ�������ۣ����ɵõ���.
�����������в���ʽ16��![]() ��17�����ɵõ��𰸣�
��17�����ɵõ��𰸣�
��1���⣺S��S1�IJ�����һ��������
��![]() ��
��![]()
��![]() ����S��S1�IJ���1.
����S��S1�IJ���1.
��2����![]()
![]()
��![]() ���൱-2m+1��0����-1��m��
���൱-2m+1��0����-1��m��![]() ʱ��
ʱ��![]() ��
��![]() ��
��
��-2m+1��0����m��![]() ʱ��
ʱ��![]() ��
��![]() ����-2m+1= 0����m =
����-2m+1= 0����m =![]() ʱ��
ʱ��![]() =
= ![]() ��
��
���ɢٵã�S1��S2��-2m+1����![]() ����mΪ����������
����mΪ����������![]() ����һ��ͼ�ε��������S1��S2֮�䣨������S1��S2�������Ϊ����������ֵ����ֻ��16������16��
����һ��ͼ�ε��������S1��S2֮�䣨������S1��S2�������Ϊ����������ֵ����ֻ��16������16��![]() ��17����
��17����![]() ��m��9����m����������m= 9��
��m��9����m����������m= 9��


 �Ͻ�ƽСѧ��������ϵ�д�
�Ͻ�ƽСѧ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������һ�����ܣ�ƽ��ÿ����۳�20�裬ÿ��ӯ��40Ԫ��Ϊ������ӯ����������ٿ�棬���Ծ�����ȡ�ʵ��Ľ��۴�ʩ�������鷢�֣����ÿ�軨��ÿ��1Ԫ������ƽ��ÿ��ɶ��۳�2�裮
��1��������ƽ��ÿ��Ҫӯ��1200Ԫ��ÿ�軨��Ӧ���۶���Ԫ��
��2��ÿ�軨�ܽ��Ͷ���Ԫʱ������ƽ��ÿ��ӯ����࣬�Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڵȱ���ABC�У�
��1����ͼ1����DΪ�߶�BC�е㣬�߶�AD����ֱ��AB�ĶԳ��߶�Ϊ�߶�AE������DE�����BDE�Ķ�����
��2������DΪ�߶�BC��һ���㣨����B��C�غϣ�������AD�����߶�AD�Ƶ�D��ʱ����ת60���õ��߶�DE������BE.
�ٸ���������ͼ2�в�ȫͼ�Σ�
��С��ͨ���۲졢��֤������²⣺�ڵ�D�˶��Ĺ����У�����CD=BE.�����С��֤��CD=BE.
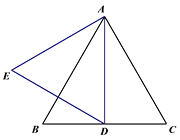
ͼ1 ͼ2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ��
��![]() ����
����![]() ΪԲ�ģ����ⳤΪ�뾶�������ֱ�
ΪԲ�ģ����ⳤΪ�뾶�������ֱ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ���ٷֱ���
���ٷֱ���![]() ��
��![]() ��ΪԲ�ģ�����
��ΪԲ�ģ�����![]() ��Ϊ�뾶�������������ڵ�
��Ϊ�뾶�������������ڵ�![]() ��������
��������![]() ����
����![]() �ڵ�
�ڵ�![]() ����֪
����֪![]() ��
��![]() ����
����![]() �ij��� ��
�ij��� ��

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ����
����![]() ��
��![]() �Ĵ��ߣ���
�Ĵ��ߣ���![]() ���ӳ�����
���ӳ�����![]() ����
����![]() ����
����![]() �Ķ���Ϊ�� ����
�Ķ���Ϊ�� ����

A.45��B.30��C.22.5��D.15��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��C�ֱ���x�ᣬy���ϣ��ı���ABCOΪ���Σ�AB=16��AC=20,��D���A����y��Գƣ���E��F�ֱ����߶�AD��AC�ϵĶ��㣨��E�����A��D�غϣ����ҡ�CEF=��ACB.
��1��ֱ��д��BC�ij����� ������D���������� ����
��2��֤������AEF����DCE���ƣ�
��3������EFCΪ����������ʱ�����E��������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������ڵ�ijһ�죬С��ȫ������8ʱ�Լ�С�����Ӽ����������ij�������ξ������森��С������ҵľ���S��ǧ�ף���ʱ��t��Сʱ���Ĺ�ϵ��ͼ��ʾ��
��1������������У��Ա������� ������������� ����
��2��������С���Ҷ�Զ��
��3��С��һ���ھ��������ʱ���Ƕ���Сʱ��
��4��С�����ҵ�ʱ���Ǽ��㣿

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�һ�κ���y=kx+b��k��b���dz�������k��0����ͼ���㣨1��0���ͣ�0��2����
��1������2��x��3ʱ����y��ȡֵ��Χ��
��2����֪��P��m��n���ڸú�����ͼ���ϣ���m��n=4�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ˮ���̳�ij��̨����ÿ̨���۷ֱ�Ϊ160Ԫ��120Ԫ��A��B�����ͺŵĵ���ȣ��±��ǽ����ܵ����������
����ʱ�� | �������� | �������� | |
A���ͺ� | B���ͺ� | ||
��һ�� | 3̨ | 4̨ | 1200Ԫ |
�ڶ��� | 5̨ | 6̨ | 1900Ԫ |
�����ۡ��ۼ۾����ֲ��䣬����=�������멁�����ɱ���
��1����A��B�����ͺŵĵ���ȵ����۵��ۣ�
��2�����̳����ò�����7500Ԫ�Ľ���ٲɹ��������ͺŵĵ���ȹ�50̨����A���ͺŵĵ��������ܲɹ�����̨��
��3���ڣ�2���������£��̳���������50̨������ܷ�ʵ������1850Ԫ��Ŀ�ꣿ���ܣ��������Ӧ�IJɹ������������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com