
【题目】如图,![]() ,
,![]() ,过
,过![]() 作
作![]() 的垂线,交
的垂线,交![]() 的延长线于
的延长线于![]() ,若
,若![]() ,则
,则![]() 的度数为( )
的度数为( )

A.45°B.30°C.22.5°D.15°
 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运12趟可完成.已知甲、乙两车单独运完此垃圾,乙车所运趟数是甲车的2倍.
(1)求甲、乙两车单独运完此堆垃圾各需运多少趟?
(2)若租用甲、乙两车各运12趟需支付运费4800元,且乙车每趟运费比甲车少200元.求单独租用一台车,租用哪台车合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB两个端点的坐标分别为A(1,-1),B(3,1),将线段AB绕点O逆时针旋转90°到对应线段CD(点A与点C对应,点B与点D对应).
(1)直接写出C,D两点的坐标;
(2)点P在x轴上,当△PCD的周长最小时,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上.
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值;
(3)若抛物线上有一动点P,使三角形ABP的面积为6,求P点坐标.
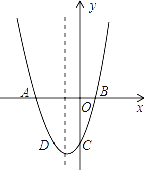
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有4个球,其中2个红球,2个白球,它们除颜色外其余都相同.
(1)摸出1个球是白球的概率是 ;
(2)同时摸两个球恰好是两个红球的概率(要求画树状图或列表).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个边长为m+3的正方形,先将这个正方形两邻边长分别增加1和减少1,得到的长方形①的面积为S1.
(1)试探究该正方形的面积S与S1的差是否是一个常数,如果是,求出这个常数;如果不是,说明理由;
(2)再将这个正方形两邻边长分别增加4和减少2,得到的长方形②的面积为S2.
①试比较S1,S2的大小;
②当m为正整数时,若某个图形的面积介于S1,S2之间(不包括S1,S2)且面积为整数,这样的整数值有且只有16个,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿DE、EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=100°,则∠C的度数为( )
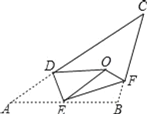
A. 40°B. 41°C. 42°D. 43°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知M是△ABC的边AB的中点,D是MC的延长线上一点,满足∠ACM=∠BDM.
(1)求证:AC=BD;
(2)若∠BMC=60°,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形OABC的顶点O在坐标原点,顶点A在x轴上,∠B=120°,OA=2,
将菱形OABC绕原点顺时针旋转105°至OA′B′C′的位置,则点B′的坐标为( )

A. (![]() ,
, ![]() ) B. (
) B. (![]() ,
, ![]() ) C. (-
) C. (-![]() ,
, ![]() ) D. (
) D. (![]() ,
, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com