
【题目】如图,已知M是△ABC的边AB的中点,D是MC的延长线上一点,满足∠ACM=∠BDM.
(1)求证:AC=BD;
(2)若∠BMC=60°,求![]() 的值.
的值.

【答案】(1)证明见解析(2)2
【解析】
(1)证明:延长CM至F,使MF=CM,连接AF、BF,根据对角线互相平分的四边形是平行四边形得到四边形AFBC是平行四边形,根据平行四边形的性质得到∠BFM=∠ACM,等量代换得到∠BFM=∠BDM,即可证明BD=BF=AC;
(2) 延长CM至点E,使EM=CD,连结AE,证明△ACE≌△BDM,根据全等三角形的性质得到AE=BM=AM,又∠BMC=60° ,证明△AEM是等边三角形,得到AB=2AM=2ME=2CD,即可求解.
(1)证明:延长CM至F,使MF=CM,连接AF、BF
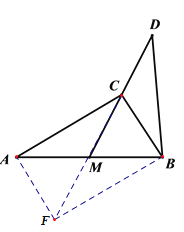
∵四边形AFBC中对角线CF、AB互相平分
∴四边形AFBC是平行四边形
∴∠BFM=∠ACM,
∵∠ACM=∠BDM.
∴∠BFM=∠BDM,
∴BD=BF=AC
(2)解:延长CM至点E,使EM=CD,连结AE
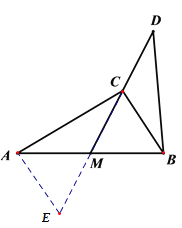
∴在△ACE和△BDM中
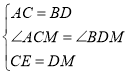
∴△ACE≌△BDM
∴AE=BM=AM
又∠BMC=60°
∴∠AME=60°
∴△AEM是等边三角形
∴AB=2AM=2ME=2CD
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】义洁中学计划从荣威公司购买A、B两种型号的小黑板,经洽谈,购买一块A型小黑板比买一块B型小黑板多用20元.且购买5块A型小黑板和4块B型小黑板共需820元.
(1)求购买一块A型小黑板、一块B型小黑板各需要多少元.
(2)根据义洁中学实际情况,需从荣威公司购买A、B两种型号的小黑板共60块,要求购买A、B两种型号小黑板的总费用不超过5240元.并且购买A型小黑板的数量应大于购买A、B种型号小黑板总数量的![]() .请你通过计算,求出义洁中学从荣威公司购买A、B两种型号的小黑板有哪几种方案.
.请你通过计算,求出义洁中学从荣威公司购买A、B两种型号的小黑板有哪几种方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节三天假期的某一天,小明全家上午8时自驾小汽车从家里出发,到某著名旅游景点游玩.该小汽车离家的距离S(千米)与时间t(小时)的关系如图所示.
(1)在这个过程中,自变量是 ,因变量是 .
(2)景点离小明家多远?
(3)小明一家在景点游玩的时间是多少小时?
(4)小明到家的时间是几点?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2).
(1)当﹣2<x≤3时,求y的取值范围;
(2)已知点P(m,n)在该函数的图象上,且m﹣n=4,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场投入13 800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:
类别/单价 | 成本价 | 销售价(元/箱) |
甲 | 24 | 36 |
乙 | 33 | 48 |
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完500箱矿泉水,该商场共获得利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高饮水质量,越来越多的居民开始选购家用净水器.一商家抓住商机,从厂家购进了A、B两种型号家用净水器共160台,A型号家用净水器进价是150元/台,B型号家用净水器进价是350元/台,购进两种型号的家用净水器共用去36000元.
(1)求A、B两种型号家用净水器各购进了多少台;
(2)为使每台B型号家用净水器的毛利润是A型号的2倍,且保证售完这160台家用净水器的毛利润不低于11000元,求每台A型号家用净水器的售价至少是多少元?(注:毛利润=售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,图中的小方格都是边长为1的正方形,△ABC与△A'B'C'是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)画出位似中心点O;
(2)直接写出△ABC与△A′B'C'的位似比;
(3)以位似中心O为坐标原点,以格线所在直线为坐标轴建立平面直角坐标系,画出△A'B'C'关于点 O中心对称的△A″B″C″,并直接写出△A″B″C″各顶点的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com