
【题目】义洁中学计划从荣威公司购买A、B两种型号的小黑板,经洽谈,购买一块A型小黑板比买一块B型小黑板多用20元.且购买5块A型小黑板和4块B型小黑板共需820元.
(1)求购买一块A型小黑板、一块B型小黑板各需要多少元.
(2)根据义洁中学实际情况,需从荣威公司购买A、B两种型号的小黑板共60块,要求购买A、B两种型号小黑板的总费用不超过5240元.并且购买A型小黑板的数量应大于购买A、B种型号小黑板总数量的![]() .请你通过计算,求出义洁中学从荣威公司购买A、B两种型号的小黑板有哪几种方案.
.请你通过计算,求出义洁中学从荣威公司购买A、B两种型号的小黑板有哪几种方案.
【答案】解:(1)购买一块A型小黑板需要l00元,购买一块8型小黑板需要l20元;(2)有两种购买方案,方案一:购买A型小黑板21块,购买8型小黑板39块;方案二:购买A型小黑板22块.购买8型小黑板38块.
【解析】
(1)设购买一块A型小黑板需要x元,购买一块B型小黑板需(x-20)元,根据购买5块A型小黑板和4块B型小黑板共需820元即可列方程求解;
(2)设购买A型小黑板m块,则购买B型小黑板(m-60)块,根据购买A、B两种型号小黑板的总费用不超过5240元,并且购买A型小黑板的数量应大于购买A、B两种型号小黑板总数量的![]() 即可列不等式组求解.
即可列不等式组求解.
解:(1)设购买一块A型小黑板需要x元,则购买一块B型小黑板需要(x-20)元
根据题意得,5x+4(x-20) =820
解得x=100
答:购买一块A型小黑板需要l00元,购买一块8型小黑板需要80元
(2)设购买A型小黑板m块,则购买B型小黑板(60-m)块.
根据题意l00m+80(60一m)≤5240 ①
m>60×![]() ②
②
解得20<m≤22
∵m为整数.∴m为21或22
当m=21时,60-m=39:当m=22时,60-m=38.有两种购买方案:
方案一:购买A型小黑板21块,购买8型小黑板39块;
方案二:购买A型小黑板22块.购买8型小黑板38块.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,矩形OABC的两边分别在x轴和y轴上,OA=![]() cm,OC=8cm,现有两动点P、Q分别从O、C同时出发,P在线段OA上沿OA方向以每秒
cm,OC=8cm,现有两动点P、Q分别从O、C同时出发,P在线段OA上沿OA方向以每秒![]() cm的速度匀速运动,Q在线段CO上沿CO方向以每秒1cm的速度匀速运动.设运动时间为t秒.
cm的速度匀速运动,Q在线段CO上沿CO方向以每秒1cm的速度匀速运动.设运动时间为t秒.
(1)用t的式子表示△OPQ的面积S;
(2)求证:四边形OPBQ的面积是一个定值,并求出这个定值;
(3)当△OPQ与△PAB和△QPB相似时,抛物线y=![]() x 2+bx+c经过B、P两点,过线段BP上一动点M作y轴的平行线交抛物线于N,当线段MN的长取最大值时,求直线MN把四边形OPBQ分成两部分的面积之比.
x 2+bx+c经过B、P两点,过线段BP上一动点M作y轴的平行线交抛物线于N,当线段MN的长取最大值时,求直线MN把四边形OPBQ分成两部分的面积之比.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运12趟可完成.已知甲、乙两车单独运完此垃圾,乙车所运趟数是甲车的2倍.
(1)求甲、乙两车单独运完此堆垃圾各需运多少趟?
(2)若租用甲、乙两车各运12趟需支付运费4800元,且乙车每趟运费比甲车少200元.求单独租用一台车,租用哪台车合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位招聘员工,采取笔试与面试相结合的方式进行,两项成绩的原始分均为100分.前5名选手的得分如下:
序号 项目 | 1 | 2 | 3 | 4 | 5 |
笔试成绩/分 | 85 | 92 | 84 | 90 | 84 |
面试成绩/分 | 90 | 88 | 86 | 90 | 80 |
根据规定,笔试成绩和面试成绩分别按一定的百分比折和成综合成绩(综合成绩的满分仍为100分)
(1)现得知1号选手的综合成绩为88分,求笔试成绩和面试成绩各占的百分比;
(2)求出其余四名选手的综合成绩,并以综合成绩排序确定前两名人选.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() .①以点
.①以点![]() 为圆心,
为圆心,![]() 长为半径画弧,分别交
长为半径画弧,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ;②在分别以
;②在分别以![]() 、
、![]() 为圆心,
为圆心,![]() 长为半径画弧,两弧交于点
长为半径画弧,两弧交于点![]() ;③连结
;③连结![]() 、
、![]() ,则四边形
,则四边形![]() 的面积为( )
的面积为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB两个端点的坐标分别为A(1,-1),B(3,1),将线段AB绕点O逆时针旋转90°到对应线段CD(点A与点C对应,点B与点D对应).
(1)直接写出C,D两点的坐标;
(2)点P在x轴上,当△PCD的周长最小时,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
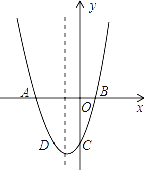
【题目】(12分)已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上.
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值;
(3)若抛物线上有一动点P,使三角形ABP的面积为6,求P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知M是△ABC的边AB的中点,D是MC的延长线上一点,满足∠ACM=∠BDM.
(1)求证:AC=BD;
(2)若∠BMC=60°,求![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com