
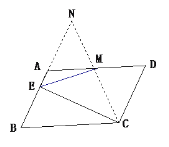
【题目】如图,在□ABCD中,BC=2AB,M是AD的中点,CE⊥AB,垂足为E,求证:∠DME=3∠AEM.

【答案】证明见解析
【解析】
设CM与BA相交于点N,证明△CMD≌△NMA ,得到AN=CD,∠ANM=∠MCD,根据BC=2AB,得到BC=BN,根据等边对等角有∠BNC=∠BCN,根据三角形外角的性质得到∠DME=∠AEM+∠EAM=∠AEM+2∠BNC,根据直角三角形斜边的中线等于斜边的一半得到EM=MN则∠AEM=∠BNC,即可证明.
如图,设CM与BA相交于点N
∵四边形ABCD是平行四边形,M是AD的中点
∴△CMD≌△NMA
∴AN=CD,
∠ANM=∠MCD,
又BC=2AB
∴BC=BN
即∠BNC=∠BCN
又∠EMD是△AEM的外角,∠EAM=∠BCD
∴∠DME=∠AEM+∠EAM
=∠AEM+∠BCD
=∠AEM+∠BCN+∠DCM
=∠AEM+∠BNC+∠DCM
=∠AEM+2∠BNC
又CE⊥AB
∴EM是Rt△CEN中斜边上的中线
∴EM=MN
∴∠AEM=∠BNC
∴∠DME=3∠AEM


科目:初中数学 来源: 题型:
【题目】某单位招聘员工,采取笔试与面试相结合的方式进行,两项成绩的原始分均为100分.前5名选手的得分如下:
序号 项目 | 1 | 2 | 3 | 4 | 5 |
笔试成绩/分 | 85 | 92 | 84 | 90 | 84 |
面试成绩/分 | 90 | 88 | 86 | 90 | 80 |
根据规定,笔试成绩和面试成绩分别按一定的百分比折和成综合成绩(综合成绩的满分仍为100分)
(1)现得知1号选手的综合成绩为88分,求笔试成绩和面试成绩各占的百分比;
(2)求出其余四名选手的综合成绩,并以综合成绩排序确定前两名人选.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有4个球,其中2个红球,2个白球,它们除颜色外其余都相同.
(1)摸出1个球是白球的概率是 ;
(2)同时摸两个球恰好是两个红球的概率(要求画树状图或列表).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿DE、EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=100°,则∠C的度数为( )
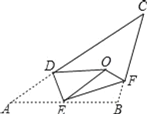
A. 40°B. 41°C. 42°D. 43°
查看答案和解析>>
科目:初中数学 来源: 题型:
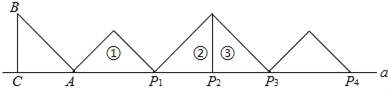
【题目】如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A顺时针旋转到位置①可得到点P1,此时AP1=![]() ;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=1+
;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=1+![]() ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3时,AP3=2+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3时,AP3=2+![]() …按此规律继续旋转,直至得到点P2018为止,则AP2018为( )
…按此规律继续旋转,直至得到点P2018为止,则AP2018为( )
A. 1345+376![]() B. 2017+
B. 2017+![]() C. 2018+
C. 2018+![]() D. 1345+673
D. 1345+673![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知M是△ABC的边AB的中点,D是MC的延长线上一点,满足∠ACM=∠BDM.
(1)求证:AC=BD;
(2)若∠BMC=60°,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小洋同学在笔记本上完成课堂练习的解题过程:
老师让同桌互相核对,同桌小宁和小洋的答案不一样,在仔细对比了自己和小洋书写的过程后,小宁说:“你在第一步出现了两个错误,导致最后错了.”小洋自己检查后发现,小宁说的是正确的.
解答下列问题:
(1)请你用标记符号“○”在以上小洋解答过程的第一步中错误之处;
(2)请重新写出完成此题的解答过程.
(2x+1)(2x﹣1)﹣(x﹣3)2
小洋的解答:
(2x+1)(2x﹣1)﹣(x﹣3)2
=(2x)2﹣1﹣(x2﹣3x+9) 第一步
=2x2﹣1﹣x2+3x﹣9 第二步
=x2+3x﹣10. 第三步
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在 Rt△ABC 中,∠ACB=90°,O为AB边上的一点,且![]() ,点D为AC边上的动点(不与点A,C 重合),将线段OD绕点O顺时针旋转90°交BC于点E.
,点D为AC边上的动点(不与点A,C 重合),将线段OD绕点O顺时针旋转90°交BC于点E.
(1)如图1,若O为AB边中点,D为AC边中点,求![]() 的值;
的值;
(2)如图2,若O为AB边中点,D不是AC边的中点,求![]() 的值。
的值。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2).
(1)当﹣2<x≤3时,求y的取值范围;
(2)已知点P(m,n)在该函数的图象上,且m﹣n=4,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com