
【题目】在等边△ABC中,
(1)如图1,若D为线段BC中点,线段AD关于直线AB的对称线段为线段AE,连接DE,求∠BDE的度数;
(2)若点D为线段BC上一动点(不与B,C重合),连接AD并将线段AD绕点D逆时针旋转60°得到线段DE,连接BE.
①根据题意在图2中补全图形;
②小玉通过观察、验证,提出猜测:在点D运动的过程中,恒有CD=BE.请帮助小玉证明CD=BE.
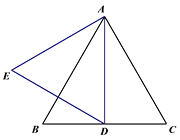
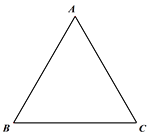
图1 图2
【答案】(1)∠EDB=30°;
(2)作图见解析,证明见解析.
【解析】试题分析:(1)首先根据题目已知条件由等腰三角形三线合一性质可以得出∠ADB=90°,∠BAD=30°,再由AD关于直线AB的对称线段为线段AE可以得出∠EAD=60°,从而可以证明△ADE是等边三角形,继而得出∠ADE=60°,最后计算出∠EDB=30°;(2)要证明CD=BE,我们可以通过证明△EAB≌△DAC证得.
试题解析:
(1)解:∵等边△ABC中, D为线段BC中点,
∴AD⊥BC,AD平分∠BAC,
即∠ADB=90°,∠BAD=30°,
∵AD关于直线AB的对称线段为线段AE,
∴AD=AE,∠EAB=∠BAD=30°,
∴∠EAD=60°,∴△EAD为等边三角形,
∴∠ADE=60°,∴∠EDB=30°;
(2)作图略,
证明:如图,连接AE.

∵AD=DE,∠ADE=60°,
∴△ADE为等边三角形,
∴AE=AD,∠EAD=60°,
∵△ABC为等边三角形,
∴∠BAC=60°,
∴∠EAD =∠BAC,
∴∠EAB=∠DAC,
在△EAB和△DAC中,
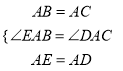 ,
,
∴△EAB≌△DAC,
∴CD=BE.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
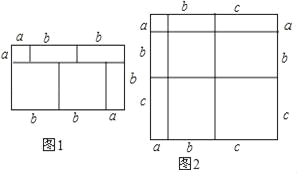
【题目】我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数字等式,例如图1,可以得到(a+2b)(a+b)=a2+3ab+2b2.请解答下问题:
(1)写出图2中所表示的数学等式_____;
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=9,ab+bc+ac=26,求a2+b2+c2的值;
(3)小明同学用2张边长为a的正方形、3张边长为b的正方形、5张边长为a、b的长方形纸片拼出了一个长方形,那么该长方形较长一边的边长为多少?
(4)小明同学又用x张边长为a的正方形,y张边长为b的正方形,z张边长分别为a、b的长方形纸片拼出了一个面积为(25a+7b)(2a+5b)长方形,求9x+10y+6.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() .①以点
.①以点![]() 为圆心,
为圆心,![]() 长为半径画弧,分别交
长为半径画弧,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ;②在分别以
;②在分别以![]() 、
、![]() 为圆心,
为圆心,![]() 长为半径画弧,两弧交于点
长为半径画弧,两弧交于点![]() ;③连结
;③连结![]() 、
、![]() ,则四边形
,则四边形![]() 的面积为( )
的面积为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB两个端点的坐标分别为A(1,-1),B(3,1),将线段AB绕点O逆时针旋转90°到对应线段CD(点A与点C对应,点B与点D对应).
(1)直接写出C,D两点的坐标;
(2)点P在x轴上,当△PCD的周长最小时,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
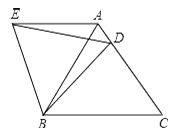
【题目】在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4.则下列四个结论:①AE∥BC;②∠ADE=∠BDC;③△BDE是等边三角形;④△AED的周长是9.其中正确的结论是__(把你认为正确结论的序号都填上.)
查看答案和解析>>
科目:初中数学 来源: 题型:
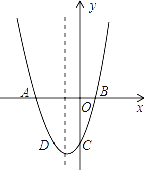
【题目】(12分)已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上.
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值;
(3)若抛物线上有一动点P,使三角形ABP的面积为6,求P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个边长为m+3的正方形,先将这个正方形两邻边长分别增加1和减少1,得到的长方形①的面积为S1.
(1)试探究该正方形的面积S与S1的差是否是一个常数,如果是,求出这个常数;如果不是,说明理由;
(2)再将这个正方形两邻边长分别增加4和减少2,得到的长方形②的面积为S2.
①试比较S1,S2的大小;
②当m为正整数时,若某个图形的面积介于S1,S2之间(不包括S1,S2)且面积为整数,这样的整数值有且只有16个,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com