练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知⊙O的半径为2，一点P到圆心O的距离为4，则点P在（　　）

    A. 圆内B. 圆上C. 圆外D. 无法确定

    【答案】C

    【解析】

    根据点与圆心的距离与半径的大小关系即可确定点P与⊙O的位置关系．

    ∵⊙O的半径分别是2，点P到圆心O的距离为4，

    ∴d＞r，

    ∴点P与⊙O的位置关系是：点在圆外，

    故选C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】小明某天上午9时骑自行车离开家，15时回家，他有意描绘了离家的距离与时间的变化情况（如图所示）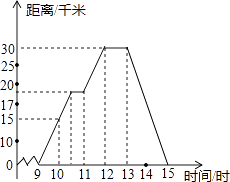
    （1）图象表示了哪两个变量的关系？哪个是自变量？哪个是因变量？
    （2）10时和13时，他分别离家多远？
    （3）他到达离家最远的地方是什么时间？离家多远？
    （4）11时到12时他行驶了多少千米？
    （5）他可能在哪段时间内休息，并吃午餐？
    （6）他由离家最远的地方返回时的平均速度是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

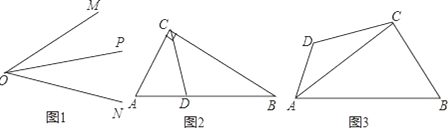
    【题目】阅读探索题：

    （1）如图1，OP是∠MON的平分线，以O为圆心任意长为半径作弧，交射线ON，OM为C，B两点，在射线OP上任取一点A（O点除外），连接AB，AC，求证：△AOB≌△AOC.

    （2）请你参考这个作全等三角形的方法，解答下列问题：

    ①如图2：在Rt△ABC中，∠ACB=90°，∠A=60°，CD平分∠ACB，试判断BC和AC、AD之间的数量关系；

    ②如图3，在四边形ABCD中，AC平分∠BAD，BC=CD=10，AC=17，AD=9，求AB的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列各数中，是近似数的是（ ）。
    A.七（1）班共有65名同学
    B.足球比赛每方共有11名球员
    C.光速是300000000米/秒
    D.小王比小华多2元

    查看答案和解析>>

    科目：初中数学 来源： 题型：

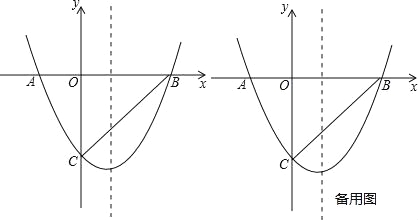
    【题目】如图，二次函数y=ax2+bx+c的图象与x轴交于点A（﹣2，0）和点B（4，0），与y轴交于点C（0，﹣4）．

    （1）求二次函数的解析式，并写出抛物线的对称轴，顶点坐标；

    （2）设E时抛物线对称轴上一点，当∠BEC=90°时，求点E的坐标；

    （3）若P（m，n）是抛物线上一个动点（其中m＞0，n＜0），是否存在这样的点P，使得△PBC的面积最大？若存在，求出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】由四舍五入法得到近似数0.09330，它的有效数字的个数是( ).
    A.3个
    B.4个
    C.5个
    D.6个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某车 间生产一批圆柱形机器零件，从中抽出了 6 件进行检验，把标准直径的长记为 0，比标准直径长的记为正数，比标准直径短的记为负数，检查记录如下：

    1

    2

    3

    4

    5

    6

    +0.2

    ﹣0.3

    ﹣0.2

    +0.3

    +0.4

    ﹣0.1

    则第_________个零件最符合标准．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读解题过程，回答问题． 如图，OC在∠AOB内，∠AOB和∠COD都是直角，且∠BOC=30°，求∠AOD的度数．
    解：过O点作射线OM，使点M，O，A在同一直线上．
    因为∠MOD+∠BOD=90°，∠BOC+∠BOD=90°，
    所以∠BOC=∠MOD，
    所以∠AOD=180°﹣∠BOC=180°﹣30°=150°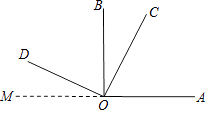

    （1）如果∠BOC=60°，那么∠AOD等于多少度？如果∠BOC=n°，那么∠AOD等于多少度？
    （2）如果∠AOB=∠DOC=x°，∠AOD=y°，求∠BOC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

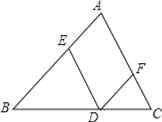
    【题目】已知D为△ABC边BC上的一个动点（不与B，C重合），过D作DE∥AC交AB于点E，作DF∥AB交AC于点F．

    （1）证明：△BDE∽△DCF；

    （2）若△ABC的面积为10，点G为线段AF上的任意一点，设FC：AC=n，△DEG的面积为S，求S关于n的关系式，并求S的最大值．

    查看答案和解析>>

    同步练习册答案