
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() 对称轴是直线
对称轴是直线![]() .
.
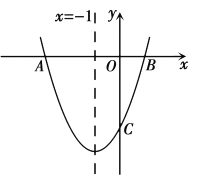
(1)求抛物线的解析式及点![]() 的坐标;
的坐标;
(2)连接![]() 是线段
是线段![]() 上一点,点
上一点,点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 正好落在
正好落在![]() 上,求点
上,求点![]() 的坐标;
的坐标;
(3)动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 运动,到达点
运动,到达点![]() 即停止运动.过点
即停止运动.过点![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() 交线段
交线段![]() 于点
于点![]() .设运动时间为
.设运动时间为![]() 秒.
秒.
①连接![]() ,若
,若![]() 与
与![]() 相似,请直接写出
相似,请直接写出![]() 的值;
的值;
②![]() 能否为等腰三角形.若能,求出
能否为等腰三角形.若能,求出![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)①t=1;②能;
;(3)①t=1;②能;![]() 秒或
秒或![]() 秒
秒
【解析】
(1)点A、B关于直线x=-1对称,AB=4,由对称性质知A(-3,0),B(1,0),将A,B两点坐标代入解析式组成方程组求解即可;
(2)先求出AC直线解析式,再将点F的坐标代入直线AC的表达式,即可求解;
(3)①当△BOC与△AMN相似,![]() =3或
=3或![]() ,即
,即![]() =3或
=3或![]() ,即可求解;②分AO=AQ、QO=AQ、AO=OQ三种情况,分别求解即可.
,即可求解;②分AO=AQ、QO=AQ、AO=OQ三种情况,分别求解即可.
解:![]() 点
点![]() 关于直线
关于直线![]() 对称,
对称,![]()
![]()
代入![]() 中,得:
中,得:![]()
解得![]()
![]() 抛物线的解析式为
抛物线的解析式为![]()
![]() 点坐标为
点坐标为![]() ;
;
![]() 如图,连接
如图,连接![]()
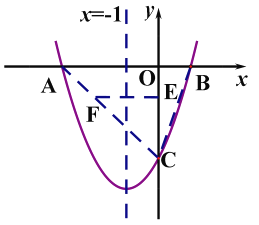
设直线![]() 的解析式为
的解析式为![]()
![]()
则有:![]()
解得![]()
![]() 直线
直线![]() 的解析式为
的解析式为![]()
![]() 点
点![]() 关于直线
关于直线![]() 对称,
对称,
又![]() 点
点![]() 到对称轴的距离为
到对称轴的距离为![]() ,
,
![]()
![]() 点的横坐标为
点的横坐标为![]()
将![]() 代入
代入![]() 中,
中,
得: ![]()
![]() ;
;
(3)①t秒时,点M的坐标为(-2t,0),则点Q(-2t,2t-3),
点N[-2t,(-2t)2+2×(-2t)-3],即(-2t,4t2-4t-3),
则MN=-4t2+4t+3,AM=3-2t,
∵△BOC与△AMN相似,
∴![]() =3或
=3或![]()
即![]() =3或
=3或![]() ,
,
解得:t=![]() 或1或-
或1或-![]() (舍去
(舍去![]() 和-
和-![]() ),
),
故t=1;
![]() 轴,
轴,
![]()
若![]() 为等腰三角形,分三种情况讨论,
为等腰三角形,分三种情况讨论,
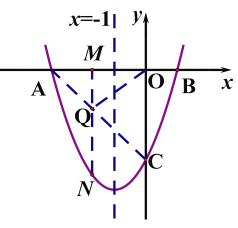
第一种情况,当![]() 时,
时,
可由![]() 定理证得
定理证得![]()
![]() 中,
中,![]() ,
,
![]()
易得![]()
![]()
第二种情况,当![]() 时,
时,
在![]() 中,
中,
![]()
![]()
![]()
即![]()
![]()
第三种情况,当![]() 时,点
时,点![]() 重合,
重合,
此时![]()
而![]() 故不符合题意,
故不符合题意,
综上所述,当![]() 秒或
秒或![]() 秒时,
秒时,![]() 为等腰三角形.
为等腰三角形.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,在
,在![]() 的角平分线
的角平分线![]() 上有一点
上有一点![]() ,将一个
,将一个![]() 角的顶点与点
角的顶点与点![]() 重合,它的两条边分别与射线
重合,它的两条边分别与射线![]() 相交于点
相交于点![]() .
.
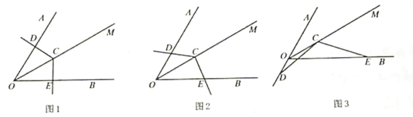
(1)如图1,当![]() 绕点
绕点![]() 旋转到
旋转到![]() 与
与![]() 垂直时,请猜想
垂直时,请猜想![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(2)当![]() 绕点
绕点![]() 旋转到
旋转到![]() 与
与![]() 不垂直时,到达图2的位置,(1)中的结论是否成立?并说明理由;
不垂直时,到达图2的位置,(1)中的结论是否成立?并说明理由;
(3)如图3,当![]() 绕点
绕点![]() 旋转到点
旋转到点![]() 位于
位于![]() 的反向延长线上时,求线段
的反向延长线上时,求线段![]() 与
与![]() 之间又有怎样的数量关系?请写出你的猜想,不需证明.
之间又有怎样的数量关系?请写出你的猜想,不需证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]()
![]() ,一次函数
,一次函数![]() ,
,
有下列结论:
①当![]() 时,
时,![]() 随
随![]() 的增大而减小;
的增大而减小;
②二次函数![]()
![]() 的图象与
的图象与![]() 轴交点的坐标为
轴交点的坐标为![]() 和
和![]() ;
;
③当![]() 时,
时,![]() ;
;
④在实数范围内,对于![]() 的同一个值,这两个函数所对应的函数值
的同一个值,这两个函数所对应的函数值![]() 均成立,则
均成立,则![]() .
.
其中,正确结论的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() 经过点
经过点![]() 和点
和点![]() .
.
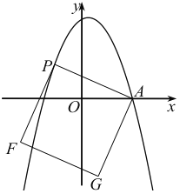
(1)求抛物线的解析式;
(2)![]() 为抛物线上的一个动点,点
为抛物线上的一个动点,点![]() 关于原点的对称点为
关于原点的对称点为![]() .当点
.当点![]() 落在该抛物线上时,求
落在该抛物线上时,求![]() 的值;
的值;
(3)![]()
![]() 是抛物线上一动点,连接
是抛物线上一动点,连接![]() ,以
,以![]() 为边作图示一侧的正方形
为边作图示一侧的正方形![]() ,随着点
,随着点![]() 的运动,正方形的大小与位置也随之改变,当顶点
的运动,正方形的大小与位置也随之改变,当顶点![]() 或
或![]() 恰好落在
恰好落在![]() 轴上时,求对应的
轴上时,求对应的![]() 点坐标.
点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为应对新型冠状病毒,某药店老板到厂家选购![]() 、
、![]() 两种品牌的医用外科口罩,
两种品牌的医用外科口罩,![]() 品牌口罩每个进价比
品牌口罩每个进价比![]() 品牌口罩每个进价多0.7元,若用7200元购进
品牌口罩每个进价多0.7元,若用7200元购进![]() 品牌的数量是用5000元购进
品牌的数量是用5000元购进![]() 品牌数量的2倍.
品牌数量的2倍.
(1)求![]() 、
、![]() 两种品牌的口罩每个进价分别为多少元?
两种品牌的口罩每个进价分别为多少元?
(2)若![]() 品牌口罩每个售价为2.1元,
品牌口罩每个售价为2.1元,![]() 品牌口罩每个售价为3元,药店老板决定一次性购进
品牌口罩每个售价为3元,药店老板决定一次性购进![]() 、
、![]() 两种品牌口罩共8000个,在这批口罩全部出售后所获利润不低于3000元.则最少购进
两种品牌口罩共8000个,在这批口罩全部出售后所获利润不低于3000元.则最少购进![]() 品牌口罩多少个?
品牌口罩多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将背面是质地、图案完全相同,正面分别标有数字-2,-1,1,2的四张卡片洗匀后,背面朝上放置在桌面上.随机抽取一张卡片,将抽取的第一张卡片上的数字作为横坐标,第二次再从剩余的三张卡片中随机抽取一张卡片,将抽取的第二张卡片上的数字作为纵坐标.
(1)请用列表法或画树状图法求出所有可能的点的坐标;
(2)求出点在x轴上方的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
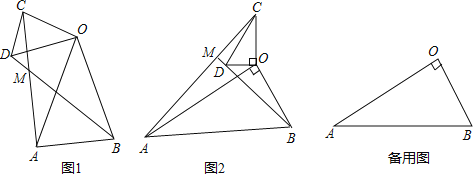
如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:
①![]() 的值为 ;
的值为 ;
②∠AMB的度数为 .
(2)类比探究
如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断![]() 的值及∠AMB的度数,并说明理由;
的值及∠AMB的度数,并说明理由;
(3)拓展延伸
在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB=![]() ,请直接写出当点C与点M重合时AC的长.
,请直接写出当点C与点M重合时AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
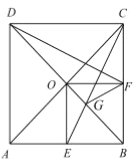
【题目】如图,在边长为1的正方形![]() 中,对角线
中,对角线![]() ,
,![]() 相交于点
相交于点![]() ,点
,点![]() ,点
,点![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,得到以下四个结论:①
,得到以下四个结论:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,其中正确的结论是________(填写序号).
,其中正确的结论是________(填写序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com