
【题目】如图①,二次函数y=ax2﹣a(b﹣1)x﹣ab(其中b<﹣1)的图象与x轴交于点A、B,与y轴交于点C(0,1),过点C的直线交x轴于点D(2,0),交抛物线于另一点E.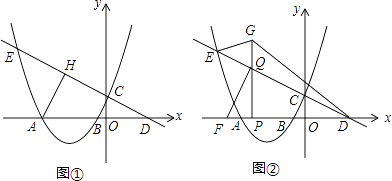
(1)用b的代数式表示a,则a=;
(2)过点A作直线CD的垂线AH,垂足为点H.若点H恰好在抛物线的对称轴上,求该二次函数的表达式;
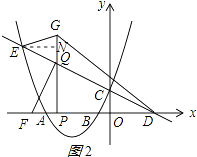
(3)如图②,在(2)的条件下,点P是x轴负半轴上的一个动点,OP=m.在点P左侧的x轴上取点F,使PF=1.过点P作PQ⊥x轴,交线段CE于点Q,延长线段PQ到点G,连接EG、DG.若tan∠GDP=tan∠FQP+tan∠QDP,试判断是否存在m的值,使△FPQ的面积和△EGQ的面积相等?若存在求出m的值,若不存在则说明理由.
【答案】
(1)解:∵二次函数y=ax2﹣a(b﹣1)x﹣ab(其中b<﹣1),C(0,1),
∴﹣ab=1,
∴a=﹣ ![]() ;
;
故答案为:﹣ ![]()
(2)
解:作HM⊥AD于M,如图1所示:
对称轴x=﹣ ![]() =﹣
=﹣ ![]() =
= ![]() ,
,
设直线CD解析式为:y=kx+n,
∵C(0,1),D(2,0),
∴ ![]() ,
,
解得: 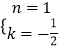 ,
,
∴直线CD解析式为:y=﹣ ![]() +1,
+1,
H在对称轴上,将x= ![]() 代入y=﹣
代入y=﹣ ![]() +1,
+1,
y=﹣ ![]() +1=
+1= ![]() ,
,
∴H( ![]() ,
, ![]() ),
),
由ax2﹣a(b﹣1)x﹣ab=0,则(ax+a)(x﹣b)=0,
∴x1=﹣1,x2=b,
∵b<﹣1,
∴A(b,0),
HM= ![]() ,
,
AM=xM﹣xA= ![]() ﹣b=﹣
﹣b=﹣ ![]() ,
,
DM=xD﹣xM=2﹣ ![]() =
= ![]() ,
,
由射影定理得:HM2=AMDM,
即( ![]() )2=﹣
)2=﹣ ![]()
![]() ,
,
解得:b=﹣3,
∵a=﹣ ![]() ,
,
∴a= ![]() ,
,
∴y= ![]() x2﹣
x2﹣ ![]() (﹣3﹣1)x+1=
(﹣3﹣1)x+1= ![]() x2+
x2+ ![]() x+1
x+1

(3)
解:存在m的值,使△FPQ的面积和△EGQ的面积相等;理由如下:
过点E作EN⊥GQ于点Q,如图2所示:
∵y= ![]() x2+
x2+ ![]() x+1与y=﹣
x+1与y=﹣ ![]() +1相交于点E,
+1相交于点E,
∴  ,
,
解得:x=﹣ ![]() ,或x=0(不合题意舍去),y=
,或x=0(不合题意舍去),y= ![]() ,
,
∴E(﹣ ![]() ,
, ![]() ),
),
∵PO=m,
∴xQ=﹣m,代入y=﹣ ![]() x+1得:yQ=
x+1得:yQ= ![]() m+1,
m+1,
∵tan∠GDP= ![]() =
= ![]() =
= ![]() ,tan∠FQP=
,tan∠FQP= ![]() ,tan∠QDP=
,tan∠QDP= ![]() ,
,
∵tan∠GDP=tan∠FQP+tan∠QDP,
∴ ![]() ,
,
∴ ![]() ,
,
∵PD=m+2,PQ= ![]() m+1,PF=1,
m+1,PF=1,
∴ ![]() ,
,
解得:QG=2,
∵△FPQ的面积= ![]() PFPQ,△EGQ的面积=
PFPQ,△EGQ的面积= ![]() QGEN,△FPQ的面积和△EGQ的面积相等,EN=
QGEN,△FPQ的面积和△EGQ的面积相等,EN= ![]() ﹣m,
﹣m,
∴ ![]() ×1×(
×1×( ![]() m+1)=
m+1)= ![]() ×2×(
×2×( ![]() ﹣m),
﹣m),
解得:m=4;
∴存在m的值,使△FPQ的面积和△EGQ的面积相等,m=4.
【解析】(1)将C(0,1)代入二次函数y=ax2﹣a(b﹣1)x﹣ab(其中b<﹣1),得出﹣ab=1,即可得出结果;(2)作HM⊥AD于M,得出对称轴x=﹣ ![]() =﹣
=﹣ ![]() =
= ![]() ,由C、D的坐标求出直线CD解析式为:y=﹣
,由C、D的坐标求出直线CD解析式为:y=﹣ ![]() +1,将x=
+1,将x= ![]() 代入y=﹣
代入y=﹣ ![]() +1,得出H(
+1,得出H( ![]() ,
, ![]() ),由ax2﹣a(b﹣1)x﹣ab=0,求出A(b,0),得出HM,AM,DM,由射影定理得:HM2=AMDM,解得b=﹣3,得出a=
),由ax2﹣a(b﹣1)x﹣ab=0,求出A(b,0),得出HM,AM,DM,由射影定理得:HM2=AMDM,解得b=﹣3,得出a= ![]() ,即可得出二次函数的表达式;(3)过点E作EN⊥GQ于点Q,由y=
,即可得出二次函数的表达式;(3)过点E作EN⊥GQ于点Q,由y= ![]() x2+
x2+ ![]() x+1与y=﹣
x+1与y=﹣ ![]() +1相交于点E,求出E(﹣
+1相交于点E,求出E(﹣ ![]() ,
, ![]() ),由PO=m,得出xQ=﹣m,yQ=
),由PO=m,得出xQ=﹣m,yQ= ![]() m+1,由tan∠GDP=
m+1,由tan∠GDP= ![]() =
= ![]() ,tan∠FQP=
,tan∠FQP= ![]() ,tan∠QDP= img src="http://thumb.zyjl.cn/questionBank/Upload/2017/07/19/20/0a7c1aa9/SYS201707192050383582795064_DA/SYS201707192050383582795064_DA.023.png" width="19" height="32" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" /> ,得出
,tan∠QDP= img src="http://thumb.zyjl.cn/questionBank/Upload/2017/07/19/20/0a7c1aa9/SYS201707192050383582795064_DA/SYS201707192050383582795064_DA.023.png" width="19" height="32" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" /> ,得出 ![]() ,求出QG=2,再由△FPQ的面积=
,求出QG=2,再由△FPQ的面积= ![]() PFPQ,△EGQ的面积=
PFPQ,△EGQ的面积= ![]() QGEN,由△FPQ的面积和△EGQ的面积相等,得出方程,解方程即可.
QGEN,由△FPQ的面积和△EGQ的面积相等,得出方程,解方程即可.
【考点精析】根据题目的已知条件,利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


科目:初中数学 来源: 题型:
【题目】如图,有一圆柱,其高为12cm,它的底面半径为3cm,在圆柱下底面A处有一只蚂蚁,它想得到上面B处的食物,则蚂蚁经过的最短距离为_________.(π取3)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,水平面上有一个坡度i=1:2的斜坡AB,矩形货柜DEFG放置在斜坡上,己知DE=2.5m.EF=2m,BF=3.5m,则点D离地面的高DH为 m.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )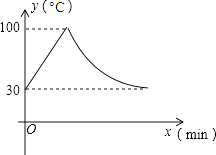
A.7:20
B.7:30
C.7:45
D.7:50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB′E,AB′与CD边交于点F,则B′F的长度为( ) 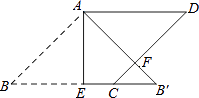
A.1
B.![]()
C.2- ![]()
D.2 ![]() ﹣2
﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
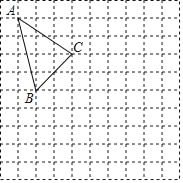
【题目】如图,在正方形网格中,每个小正方形的边长为1,格点△ABC(顶点在网格线的交点上)的顶点A、C的坐标分别为A(﹣3,4)C(0,2)
(1)请在网格所在的平面内建立平面直角坐标系,并写出点B的坐标;
(2)画出△ABC关于原点对称的图形△A1B1C1;
(3)求△ABC的面积;
(4)在x轴上存在一点P,使PA+PB的值最小,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某剧院的观众席的座位为扇形,且按下列分式设置:
排数(x) | 1 | 2 | 3 | 4 | … |
座位数(y) | 50 | 53 | 56 | 59 | … |
(1)按照上表所示的规律,当x每增加1时,y如何变化?
(2)写出座位数y与排数x之间的关系式;
(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高空抛物极其危险,是我们必须杜绝的行为.据研究,高空抛物下落的时间t(单位:s)和高度 h(单位:m)近似满足公式 t=![]() (不考虑风速的影响)
(不考虑风速的影响)
(1)从 50m 高空抛物到落地所需时间 t1 是多少 s,从 100m 高空抛物到落地所 需时间 t2 是多少 s;
(2)t2 是 t1 的多少倍?
(3)经过 1.5s,高空抛物下落的高度是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com