
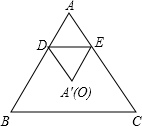
 如图,等边三角形ABC中,AB=3,点D,E分别在AB,AC上,且DE∥BC,沿直线DE折叠△ABC,当点A的对应点A′与△ABC的中心O重合时,折痕DE的长为1.
如图,等边三角形ABC中,AB=3,点D,E分别在AB,AC上,且DE∥BC,沿直线DE折叠△ABC,当点A的对应点A′与△ABC的中心O重合时,折痕DE的长为1. 分析 如图所示,过点O作OF⊥AC,垂足为F.连接OA=OC.先求得AO的长,由翻折的性质可知AG=$\frac{1}{2}AO$,然后可求得∠ADE=60°,最后根据特殊锐角三角函数值可求得DG的长度,从而可求得DE的长.
解答 解:如图所示,过点O作OF⊥AC,垂足为F.连接OA=OC.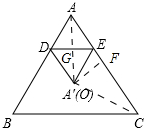
∵点O为等边三角形的中心,
∴OA=OC.∠OAF=30°.
又∵OF⊥AC,
∴AF=CF=1.5
∴OA=$\frac{AF}{cos30°}$=$\frac{3}{2}×\frac{2}{\sqrt{3}}$=$\sqrt{3}$.
由翻折的性质可知:AG=$\frac{1}{2}AO$=$\frac{\sqrt{3}}{2}$.
∵DE∥BC,
∴∠ADG=∠B=60°.
∴$\frac{AG}{DG}=\sqrt{3}$,即$\frac{\frac{\sqrt{3}}{2}}{DG}=\sqrt{3}$.
∴DG=$\frac{1}{2}$.
∴DE=1.
故答案为:1.
点评 本题主要考查的是翻折的性质、特殊锐角三角函数值,由点A′与等边三角形的中线重合求得AF、OA的长是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
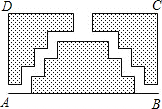 如图是一块长方形ABCD的场地,长AB=(3a+2)米,宽AD为(a+1)米,从A、B两处入口的小路宽都为1米,两小路汇合处路宽为2米,其余部分种植草坪,则草坪面积为3a2 平方米.
如图是一块长方形ABCD的场地,长AB=(3a+2)米,宽AD为(a+1)米,从A、B两处入口的小路宽都为1米,两小路汇合处路宽为2米,其余部分种植草坪,则草坪面积为3a2 平方米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com