
分析 (1)根据方程的系数结合根的判别式,即可得出△=4m+17>0,解之即可得出结论;
(2)设方程的两根分别为a、b,根据根与系数的关系结合菱形的性质,即可得出关于m的一元二次方程,解之即可得出m的值,再根据a+b=-2m-1>0,即可确定m的值.
解答 解:(1)∵方程x2+(2m+1)x+m2-4=0有两个不相等的实数根,
∴△=(2m+1)2-4(m2-4)=4m+17>0,
解得:m>-$\frac{17}{4}$.
∴当m>-$\frac{17}{4}$时,方程有两个不相等的实数根.
(2)设方程的两根分别为a、b,
根据题意得:a+b=-2m-1,ab=m2-4.
∵2a、2b为边长为5的菱形的两条对角线的长,
∴a2+b2=(a+b)2-2ab=(-2m-1)2-2(m2-4)=2m2+4m+9=52=25,
解得:m=-4或m=2.
∵a>0,b>0,
∴a+b=-2m-1>0,
∴m=-4.
若边长为5的菱形的两条对角线的长分别为方程两根的2倍,则m的值为-4.
点评 本题考查了根的判别式、根与系数的关系、菱形的性质以及解一元二次方程,解题的关键是:(1)根据方程的系数结合根的判别式,找出△=4m+17>0;(2)根据根与系数的关系结合菱形的性质,找出关于m的一元二次方程.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:解答题
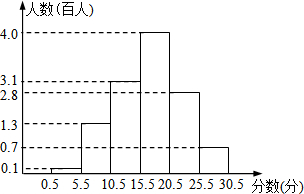 2017年3月27日是第22个全国中小学生安全教育日,某校为增强学生的安全意识,组织全校学生参加安全知识测试,并对测试成绩做了详细统计,将测试成绩(成绩都是整数,试卷满分30分)绘制成了如下“频数分布直方图”,请回答:
2017年3月27日是第22个全国中小学生安全教育日,某校为增强学生的安全意识,组织全校学生参加安全知识测试,并对测试成绩做了详细统计,将测试成绩(成绩都是整数,试卷满分30分)绘制成了如下“频数分布直方图”,请回答:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
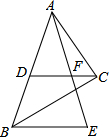 如图,Rt△ABC中,∠ACB=90°,斜边AB=9,D为AB的中点,F为CD上一点,且CF=$\frac{1}{3}$CD,过点B作BE∥DC交AF的延长线于点E,则BE的长为( )
如图,Rt△ABC中,∠ACB=90°,斜边AB=9,D为AB的中点,F为CD上一点,且CF=$\frac{1}{3}$CD,过点B作BE∥DC交AF的延长线于点E,则BE的长为( )| A. | 6 | B. | 4 | C. | 7 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
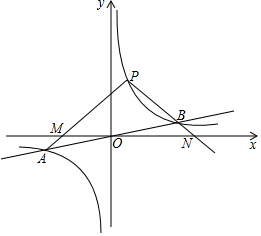 如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=$\frac{1}{4}$x的图象交于点A,B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.
如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=$\frac{1}{4}$x的图象交于点A,B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 无限小数是无理数 | B. | $\sqrt{16}$的平方根是±4 | ||
| C. | -6是(-6)2的一个算术平方根 | D. | -5的立方根是$\root{3}{-5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com