
【题目】如图,将平行四边形ABCD的边DC延长至点E , 使CE=DC , 连接AE , 交BC于点F . 
(1)求证:△ABF≌△ECF;
(2)连接AC、BE , 则当∠AFC与∠D满足什么条件时,四边形ABEC是矩形?请说明理由
【答案】
(1)
解答:证明:在平行四边形ABCD中,AB∥CD,AB=CD,
∴∠BAE=∠AEC,又∵CE=CD,
∴AB=CE,在△ABF和△ECF中,  ,
,
∴△ABF≌△ECF(AAS).
(2)
解答:解:当∠AFC=2∠D时,四边形ABEC是矩形,理由如下:
∵四边形ABCD是平行四边形,
∴BC∥AD,AB∥DC,AB=DC,
∴∠BCE=∠D,AB∥EC,
又∵CE=DC,
∴四边形ABEC是平行四边形,
∵∠AFC=∠FEC+∠BCE,
∴当∠AFC=2∠D时,则有∠FEC=∠FCE,
∴FC=FE,
∴四边形ABEC是矩形.
【解析】(1)由四边形ABCD是平行四边形,CE=DC , 易证得∠ABF=∠ECF , ∠AFB=∠EFC , AB=EC , 则可证得△ABF≌△ECF;(2)首先根据四边形ABCD是平行四边形,得到四边形ABEC是平行四边形,然后证得FC=FE , 利用对角线互相相等的四边形是矩形判定四边形ABEC是矩形.
【考点精析】认真审题,首先需要了解平行四边形的性质(平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分),还要掌握矩形的判定方法(有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形)的相关知识才是答题的关键.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,P为边BC上一动点,PE⊥AB于E , PF⊥AC于F , 动点P从点B出发,沿着BC匀速向终点C运动,则线段EF的值大小变化情况是( ).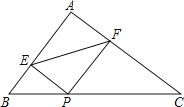
A.一直增大
B.一直减小
C.先减小后增大
D.先增大后减少
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是
A.三个角的度数之比为1∶3∶4的三角形是直角三角形
B.三个角的度数之比为3∶4∶5的三角形是直角三角形
C.三边长度之比为3∶4∶5的三角形是直角三角形
D.三边长度之比为5∶12∶13的三角形是直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() (a>0,a为常数)和y=
(a>0,a为常数)和y=![]() 在第一象限内的图象如图所示,点M在y=
在第一象限内的图象如图所示,点M在y=![]() 的图象上,MC⊥x轴于点C,交y=
的图象上,MC⊥x轴于点C,交y=![]() 的图象于点A;MD⊥y轴于点D,交y=
的图象于点A;MD⊥y轴于点D,交y=![]() 的图象于点B,当点M在y=
的图象于点B,当点M在y=![]() 的图象上运动时,以下结论:
的图象上运动时,以下结论:
①S△ODB=S△OCA;
②四边形OAMB的面积不变;
③当点A是MC的中点时,则点B是MD的中点.
其中正确结论的个数是( )

A.0 B.1 C.2 D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列条件中,能得到DG∥BC的是( )
A.CD⊥AB,EF⊥AB
B.∠1=∠2
C.∠1=∠2,∠4+∠5=180°
D.CD⊥AB,EF⊥AB,∠1=∠2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com