
【题目】如图,点![]() 在
在![]() 的边
的边![]() 上,点
上,点![]() 在
在![]() 内部,
内部,![]() ,
,![]() ,
,![]() .
.
给出下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的有( )
.其中正确的有( )

A. 1个B. 2个C. 3个D. 4个
【答案】D
【解析】
①由AB=AC,AD=AE,利用等式的性质得到夹角相等,利用SAS得出△BAD≌△CAE,由全等三角形的对应边相等得到BD=CE;②由等腰直角三角形的性质得到∠ABE+∠ECB=45°,等量代换得到∠ABD+∠ECB=45°;③由∠ABD+∠ECB=45°以及∠ABC=45°得到∠ABD+∠ECB+∠ABC=90°,从而得到∠BEC=90°,即可得到BD垂直于CE;④由BD垂直于CE,在直角三角形BCE和三角形CDE中,利用勾股定理列出关系式,等量代换即可作出判断.
①∵∠DAE=∠BAC=90°,
∴∠BAC+∠BAE=∠DAE+∠BAE,即∠BAD=∠CAE,
又∵AB=AC, AD=AE,
∴△BAD≌△CAE(SAS),
∴BD=CE,故①正确;
∵△BAD≌△CAE,
∴∠ABD=∠ACE,
∵AB=AC,∠BAC=90°,
∴∠ACB=∠ABC=45°,即∠ACE+∠BCE=45°,
∴∠ABD+∠ECB=45°,故②正确;
∴∠ABD+∠ECB+∠ABC=90°,
∴∠BEC=90°,即BD⊥CE,故③正确;
∴CD2=CE2+DE2,BE2+ CE2=BC2,
即CE2=CD2-DE2,BE2=BC2-CE2,
又∵AB=AC,∠BAC=90°,AD=AE,∠DAE=90°,
∴BC2=AB2+AC2=2AB2,DE2=AD2+AE2=2AD2,
∴BE2=BC2-CE2=2AB2-(CD2-2AD2)=2(AD2+AB2)-CD2,故④正确,
∴正确的有4个,
故选D.


科目:初中数学 来源: 题型:
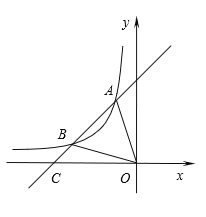
【题目】如图,一次函数y=x+4的图像与反比例函数![]() (k为常数且k≠0)的图像交于A(-1,a),B(b,1)两点,与x轴交于点C.
(k为常数且k≠0)的图像交于A(-1,a),B(b,1)两点,与x轴交于点C.
(1)求此反比例函数的表达式;
(2)若点P在x轴上,且![]() ,求点P的坐标.
,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国庆节放假时,小华一家三口一起乘小轿车去乡下探望爷爷、奶奶和外公、外婆.早上从家里出发,向东走了4千米到超市买东西,然后又向东走了3千米到爷爷家,中午从爷爷家出发向西走了12千米到外公家,晚上返回家里.
![]()
(1)若以家为原点,向东为正方向,用1个单位长度表示1千米,请将超市、爷爷家和外公家的位置在下面数轴上分别用点A、B、C表示出来;
(2)若小轿车每千米耗油0.09升,求小明一家从出发到返回家所经历路程小车的耗油量.(精确到0.1升)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]() ;
;
(2)![]() ;
;
(3)(-36)÷(+12)-(-4)×(-0.5);
(4)(1-![]() +
+![]() )×(-48);
)×(-48);
(5)![]() ;
;
(6)![]() ;
;
(7)![]() ;
;
(8)18+42÷(-2)-(-3)2×5;
(9)![]() ×[-32÷(-
×[-32÷(-![]() )2+(-2)3] ;
)2+(-2)3] ;
(10)![]() ;
;
(11)![]()
(12)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=11,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点E,则DF的长为( )

A. 4.5 B. 5 C. 5.5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,直线y=-![]() x+3与x轴相交于点A,与y轴相交于点B,点C(m,n)是第二象限内一点,以点C为圆心的圆与x轴相切于点E,与直线AB相切于点F.
x+3与x轴相交于点A,与y轴相交于点B,点C(m,n)是第二象限内一点,以点C为圆心的圆与x轴相切于点E,与直线AB相切于点F.
(1)当四边形OBCE是矩形时,求点C的坐标;
(2)如图②,若⊙C与y轴相切于点D,求⊙C的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上运动(
上运动(![]() 不与
不与![]() 、
、![]() 重合),连接
重合),连接![]() ,作
,作![]() ,
,![]() 交线段
交线段![]() 于
于![]() .
.


(1)当![]() 时,
时,![]() = ,
= ,![]() = ;点
= ;点![]() 从
从![]() 向
向![]() 运动时,
运动时,![]() 逐渐 (填“增大”或“减小”);
逐渐 (填“增大”或“减小”);
(2)当![]() 等于多少时,
等于多少时,![]() ,请说明理由;
,请说明理由;
(3)在点![]() 的运动过程中,
的运动过程中,![]() 的形状可以是等腰三角形吗?若可以,请直接写出
的形状可以是等腰三角形吗?若可以,请直接写出![]() 的度数.若不可以,请说明理由.
的度数.若不可以,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=a![]() -4x+c的图像经过点A和点B.
-4x+c的图像经过点A和点B.

(1)求该二次函数的表达式;
(2)写出该抛物线的对称轴及顶点坐标;
(3)点P(m,m)与点Q均在该函数图像上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q到x轴的距离
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,等腰Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3,3),点C的坐标为(1,0),点P为斜边OB上的一个动点,则PA+PC的最小值为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com