
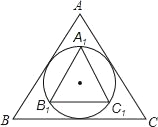
【题目】如图,若等边△A1B1C1内接于等边△ABC的内切圆,则![]() 的值为_____.
的值为_____.
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:
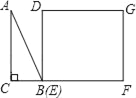
【题目】如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,DE=2![]() cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
A. 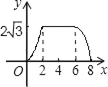 B.
B. 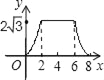 C.
C. 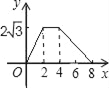 D.
D. 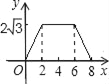
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形A1B1C1O,A2B2C2C1,A3B3C3C2, ……,按如图的方式放置。点A1,A2,A3,……和点C1,C2,C3……分别在直线y=x +1和x轴上,则点A6的坐标是____________.
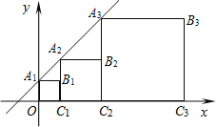
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形 ABCD 中,AB=1,BC=![]() ,点 M 在 AC 上,且 AM=
,点 M 在 AC 上,且 AM=![]() AC,连接并延长 BM 交 AD 于点 N.
AC,连接并延长 BM 交 AD 于点 N.
(1)求证:△ABC∽△AMB;
(2)求 MN 的长.
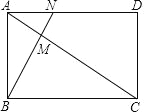
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大酒店共有豪华间 50 间,实行旅游淡季、旺季两种价格标准:
淡季 | 旺季 | |
豪华间价格(元/天) | 600 | 800 |
(1)该酒店去年淡季,开始时,平均每天入住房间数为 20 间,后来,实行降价优惠提高豪华间入住率,每降低 20 元,每天入住房间数增加 1 间.如果豪华间的某日总收入为 12500 元,则该天的豪华间实际每间价格为多少元(同天的房间价格相同);
(2)该酒店豪华间的间数不变.经市场调查预测,如果今年旺季豪华间实行旺季价格,那么每天都客满;如果价格继续上涨,那么每增加 25 元,每天未入住房间数增加 1 间.不考虑其他因素,该酒店将豪华间的价格上涨多少元时, 豪华间的日总收入最高?最高日总收入是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网瘾低龄化问题已经引起社会各界的高度关注,有关部门在全国范围内对12﹣35岁的网瘾人群进行了简单的随机抽样调查,绘制出以下两幅统计图.

请根据图中的信息,回答下列问题:
(1)这次抽样调查中共调查了 人;
(2)请补全条形统计图;
(3)扇形统计图中18﹣23岁部分的圆心角的度数是 ;
(4)据报道,目前我国12﹣35岁网瘾人数约为2000万,请估计其中12﹣23岁的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,点D为⊙O上一点,且CD=CB、连接DO并延长交CB的延长线于点E.
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)若BE=4,DE=8,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
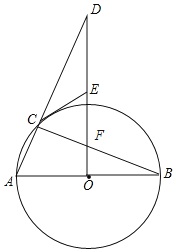
【题目】如图,AB是⊙O的直径,DO⊥AB于点O,连接DA交⊙O于点C,过点C作⊙O的切线交DO于点E,连接BC交DO于点F.
(1)求证:CE=EF;
(2)连接AF并延长,交⊙O于点G.填空:
①当∠D的度数为 时,四边形ECFG为菱形;
②当∠D的度数为 时,四边形ECOG为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=(x+2)2+m的图象与y轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(﹣1,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足(x+2)2+m≥kx+b的x的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com