
【题目】如图,AB是⊙O的直径,DO⊥AB于点O,连接DA交⊙O于点C,过点C作⊙O的切线交DO于点E,连接BC交DO于点F.
(1)求证:CE=EF;
(2)连接AF并延长,交⊙O于点G.填空:
①当∠D的度数为 时,四边形ECFG为菱形;
②当∠D的度数为 时,四边形ECOG为正方形.
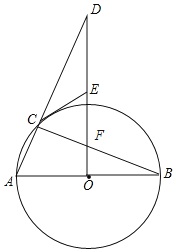
【答案】(1)证明见解析;(2)①30°;②22.5°.
【解析】(1)连接OC,如图,利用切线的性质得∠1+∠4=90°,再利用等腰三角形和互余证明∠1=∠2,然后根据等腰三角形的判定定理得到结论;
(2)①当∠D=30°时,∠DAO=60°,证明△CEF和△FEG都为等边三角形,从而得到EF=FG=GE=CE=CF,则可判断四边形ECFG为菱形;
②当∠D=22.5°时,∠DAO=67.5°,利用三角形内角和计算出∠COE=45°,利用对称得∠EOG=45°,则∠COG=90°,接着证明△OEC≌△OEG得到∠OEG=∠OCE=90°,从而证明四边形ECOG为矩形,然后进一步证明四边形ECOG为正方形.
(1)证明:连接OC,如图,
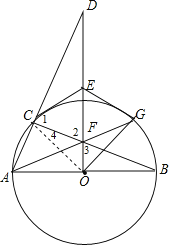 .
.
∵CE为切线,
∴OC⊥CE,
∴∠OCE=90°,即∠1+∠4=90°,
∵DO⊥AB,
∴∠3+∠B=90°,
而∠2=∠3,
∴∠2+∠B=90°,
而OB=OC,
∴∠4=∠B,
∴∠1=∠2,
∴CE=FE;
(2)解:①当∠D=30°时,∠DAO=60°,
而AB为直径,
∴∠ACB=90°,
∴∠B=30°,
∴∠3=∠2=60°,
而CE=FE,
∴△CEF为等边三角形,
∴CE=CF=EF,
同理可得∠GFE=60°,
利用对称得FG=FC,
∵FG=EF,
∴△FEG为等边三角形,
∴EG=FG,
∴EF=FG=GE=CE,
∴四边形ECFG为菱形;
②当∠D=22.5°时,∠DAO=67.5°,
而OA=OC,
∴∠OCA=∠OAC=67.5°,
∴∠AOC=180°-67.5°-67.5°=45°,
∴∠AOC=45°,
∴∠COE=45°,
利用对称得∠EOG=45°,
∴∠COG=90°,
易得△OEC≌△OEG,
∴∠OEG=∠OCE=90°,
∴四边形ECOG为矩形,
而OC=OG,
∴四边形ECOG为正方形.
故答案为30°,22.5°.


科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,CE=2,连接CF,以下结论:①△ABF≌△CBF;②点E到AB的距离是2![]() ;③tan∠DCF=
;③tan∠DCF=![]() ;④△ABF的面积为
;④△ABF的面积为![]() .其中一定成立的有几个( )
.其中一定成立的有几个( )
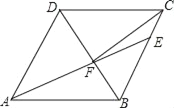
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
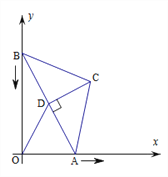
【题目】如图,在△ABC中,BC=AC=5,AB=8,CD为AB边的高,点A在x轴上,点B在y轴上,点C在第一象限,若A从原点出发,沿x轴向右以每秒1个单位长的速度运动,则点B随之沿y轴下滑,并带动△ABC在平面内滑动,设运动时间为t秒,当B到达原点时停止运动
(1)连接OC,线段OC的长随t的变化而变化,当OC最大时,t=____;
(2)当△ABC的边与坐标轴平行时,t=____。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.有且只有一条直线与已知直线垂直;
B.从直线外一点到这条直线的垂线段,叫做这点到这条直线距离;
C.互相垂直的两条线段一定相交;
D.直线![]() 外一点
外一点![]() 与直线
与直线![]() 上各点连接而成的所有线段中,最短线段的长度是
上各点连接而成的所有线段中,最短线段的长度是![]() ,则点
,则点![]() 到直线
到直线![]() 的距离是
的距离是![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MAN=90°,点C在边AM上,AC=4,点B为边AN上一动点,连接BC,△A′BC与△ABC关于BC所在直线对称,点D,E分别为AC,BC的中点,连接DE并延长交A′B所在直线于点F,连接A′E.当△A′EF为直角三角形时,AB的长为_____.
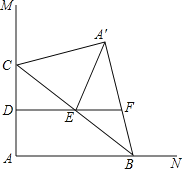
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+6x+c交x轴于A,B两点,交y轴于点C.直线y=x﹣5经过点B,C.
(1)求抛物线的解析式;
(2)过点A的直线交直线BC于点M.
①当AM⊥BC时,过抛物线上一动点P(不与点B,C重合),作直线AM的平行线交直线BC于点Q,若以点A,M,P,Q为顶点的四边形是平行四边形,求点P的横坐标;
②连接AC,当直线AM与直线BC的夹角等于∠ACB的2倍时,请直接写出点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,直线a,b,c分别通过A、D、C三点,且a∥b∥c.若a与b之间的距离是5,b与c之间的距离是7,则正方形ABCD的面积是( )
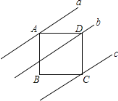
A.70B.74C.144D.148
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 图象与x轴交于A,B两点,对称轴为直线x=2,下列结论:①abc>0; ②4a+b=0;③若点A坐标为(1,0),则线段AB=5; ④若点M(x1,y1)、N(x2,y2)在该函数图象上,且满足0<x1<1,2<x2<3,则y1<y2其中正确结论的序号为( )
图象与x轴交于A,B两点,对称轴为直线x=2,下列结论:①abc>0; ②4a+b=0;③若点A坐标为(1,0),则线段AB=5; ④若点M(x1,y1)、N(x2,y2)在该函数图象上,且满足0<x1<1,2<x2<3,则y1<y2其中正确结论的序号为( )
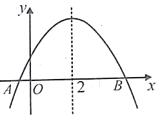
A. ①,② B. ②,③ C. ③,④ D. ②,④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某驻村扶贫小组为解决当地贫困问题,带领大家致富.经过调查研究,他们决定利用当地生产的甲乙两种原料开发A,B两种商品,为科学决策,他们试生产A、B两种商品100千克进行深入研究,已知现有甲种原料293千克,乙种原料314千克,生产1千克A商品,1千克B商品所需要的甲、乙两种原料及生产成本如下表所示.
甲种原料(单位:千克) | 乙种原料(单位:千克) | 生产成本(单位:元) | |
A商品 | 3 | 2 | 120 |
B商品 | 2.5 | 3.5 | 200 |
设生产A种商品x千克,生产A、B两种商品共100千克的总成本为y元,根据上述信息,解答下列问题:
(1)求y与x的函数解析式(也称关系式),并直接写出x的取值范围;
(2)x取何值时,总成本y最小?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com