
【题目】如图,将矩形ABCD置于平面直角坐标系中,其中AD边在x轴上,AB=2,直线MN:y=x﹣4沿x轴的负方向以每秒1个单位的长度平移,设在平移过程中该直线被矩形ABCD的边截得的线段长度为m,平移时间为t,m与t的函数图象如图2所示.
(1)点A的坐标为 , 矩形ABCD的面积为;
(2)求a,b的值;
(3)在平移过程中,求直线MN扫过矩形ABCD的面积S与t的函数关系式,并写出自变量t的取值范围.
【答案】
(1)(1,0);8
(2)
解:如图1所示;当直线MN经过点B时,直线MN交DA于点E.
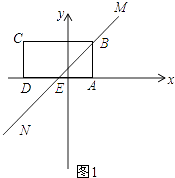
∵点A的坐标为(1,0),
∴点B的坐标为(1,2)
设直线MN的解析式为y=x+c,
将点B的坐标代入得;1+c=2.
∴c=1.
∴直线MN的解析式为y=x+1.
将y=0代入得:x+1=0,解得x=﹣1,
∴点E的坐标为(﹣1,0).
∴BE= ![]() =
= ![]() =2
=2 ![]() .
.
∴a=2 ![]()
如图2所示,当直线MN经过点C时,直线MN交x轴于点F.
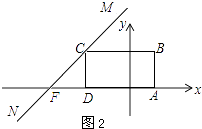
∵点D的坐标为(﹣3,0),
∴点C的坐标为(﹣3,2).
设MN的解析式为y=x+d,将(﹣3,2)代入得:﹣3+d=2,解得d=5.
∴直线MN的解析式为y=x+5.
将y=0代入得x+5=0,解得x=﹣5.
∴点F的坐标为(﹣5,0).
∴b=4﹣(﹣5)=9
(3)
解:当0≤t<3时,直线MN与矩形没有交点.
∴s=0.
当3≤t<5时,如图3所示;
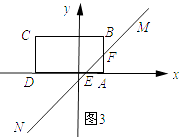
S= ![]() =
= ![]() =
= ![]() ;
;
当5≤t<7时,如图4所示:过点B作BG∥MN.
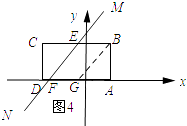
由(2)可知点G的坐标为(﹣1,0).
∴FG=t﹣5.
∴S=SBEFG+SABG=2(t﹣5)+ ![]() =2t﹣8.
=2t﹣8.
当7≤t≤9时,如图5所示.
FD=t﹣7,CF=2﹣DF=2﹣(t﹣7)=9﹣t.
S=SABCD﹣SCEF=8﹣ ![]() =
= ![]() .
.
综上所述,S与t的函数关系式为S= 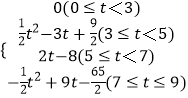
【解析】解:(1)令直线y=x﹣4的y=0得:x﹣4=0,解得:x=4,
∴点M的坐标为(4,0).
由函数图象可知:当t=3时,直线MN经过点A,
∴点A的坐标为(1,0)
沿x轴的负方向平移3个单位后与矩形ABCD相交于点A,
∵y=x﹣4沿x轴的负方向平移3个单位后直线的解析式是:y=x+3﹣4=x﹣1,
∴点A的坐标为 (1,0);
由函数图象可知:当t=7时,直线MN经过点D,
∴点D的坐标为(﹣3,0).
∴AD=4.
∴矩形ABCD的面积=ABAD=4×2=8.
【考点精析】本题主要考查了图形的平移和平移的性质的相关知识点,需要掌握对应线段,对应点所连线段平行(或在同一直线上)且相等;对应角相等;平移方向和距离是它的两要素;①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等才能正确解答此题.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E为BC边上的一点,且AE与DE分别平分∠BAD和∠ADC
(1)求证:AE⊥DE;
(2)设以AD为直径的半圆交AB于F,连结DF交AE于G,已知CD=5,AE=8.
①求BC的长;
②求 ![]() 值.
值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图: 
根据以上信息,整理分析数据如下:
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 | a | 7 | 7 | 1.2 |
乙 | 7 | b | 8 | c |
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长; 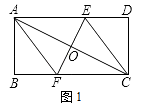
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,
①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
②若点P、Q的运动路程分别为a、b(单位:cm,ab≠0),已知A、C、P、Q四点为顶点的四边形是平行四边形,求a与b满足的数量关系式.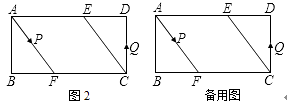
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一期间,小红到美丽的世界地质公园湖光岩参加社会实践活动,在景点P处测得景点B位于南偏东45°方向;然后沿北偏东60°方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与B之间的距离.(结果精确到0.1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线对称轴l与x轴相交于点M.
(1)求抛物线的解析式和对称轴;
(2)点P在抛物线上,且以A、O、M、P为顶点的四边形四条边的长度为四个连续的正整数,请你直接写出点P的坐标;
(3)连接AC.探索:在直线AC下方的抛物线上是否存在一点N,使△NAC的面积最大?若存在,请你求出点N的坐标;若不存在,请你说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com