
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ���y=-x2+bx+c��ͼ����x�ύ��A��B���㣬��y�ύ��C��0��3����A����ԭ�����࣬B�������Ϊ��3��0������P����������һ�����㣬����ֱ��BC���Ϸ���
��1����������κ����ı���ʽ��
��2������PO��PC�����ѡ�POC��CO���ۣ��õ��ı���POP��C����ô�Ƿ���ڵ�P��ʹ�ı���POP��CΪ���Σ������ڣ��������ʱ��P�����ꣻ�������ڣ���˵�����ɣ�
��3������P�˶���ʲôλ��ʱ���ı��� ABPC�������������ʱ��P��������ı�����������ֵ��
���𰸡�
��1���⣺��B��C������������� ![]() �����
����� ![]() ��
��
���Զ��κ����ı���ʽΪy=��x2+2x+3
��2���⣺��ͼ��
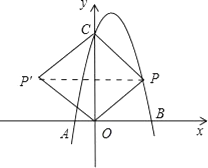
���ڵ�P��ʹ�ı���POP��CΪ���Σ�
��P������Ϊ��x����x2+2x+3����PP�佻CO��E��
���ı���POPC�����Σ�����PC=PO��
����PP��PE��CO��E��
��OE=CE= ![]() ��
��
��y= ![]() ��
��
��-x2+2x+3= ![]() ��
��
���x1= ![]() ��x2=
��x2= ![]() ���������⣬��ȥ����
���������⣬��ȥ����
��P��������� ![]() ��
�� ![]() ����
����
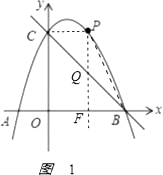
��3���⣺��ͼ1��
 ��
��
����P��y���ƽ������BC���ڵ�Q����OB���ڵ�F����P��x����x2+2x+3��
�ã�ֱ��BC�Ľ���ʽΪy=��x+3��
��Q���������x����x+3����
PQ=��x2+3x��
S�ı���ABPC=S��ABC+S��BPQ+S��CPQ= ![]() ABOC+
ABOC+ ![]() QPBF+
QPBF+ ![]() QPOF=
QPOF= ![]() ��4��3+
��4��3+ ![]() ����x2+3x����3=��
����x2+3x����3=�� ![]() ��x��
��x�� ![]() ��2+
��2+ ![]() ��
��
��x= ![]() ʱ���ı���ABPC��������
ʱ���ı���ABPC��������
��ʱP�������Ϊ�� ![]() ��
�� ![]() �����ı���ABPC��������ֵΪ
�����ı���ABPC��������ֵΪ ![]() ��
��
����������1�����ô���ϵ��������C����B��������뺯������ʽ������������
��2��Ҫʹ�ı���POP��CΪ���Σ���˸������εĶԽ�����ƽ�֣��ɵõ�P��������꣬���ݺ���ֵ���Ա����Ķ�Ӧ��ϵ���������̿ɵô𰸡���3������P��y���ƽ������BC���ڵ�Q����OB���ڵ�F�������ֱ��BC�ĺ�������ʽ����������������ʽ���P�����꣬�ٱ�ʾ����Q�����꣬���ɱ�ʾ��PQ�ij����ٸ���S�ı���ABPC=S��ABC+S��BPQ+S��CPQ��������������ʽ���Ϳ������ʱ��P��������ı�����������ֵ��
�����㾫��������ȷ��һ�κ����ı���ʽ�Ͷ��κ�������ֵ����Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪ȷ��һ��һ�κ�������Ҫȷ��һ�κ�������ʽy=kx+b��k������0���еij���k��b�������������һ�㷽���Ǵ���ϵ����������Ա�����ȡֵ��Χ��ȫ��ʵ������ô�����ڶ��㴦ȡ�����ֵ������Сֵ��������x=-b/2aʱ��y��ֵ=(4ac-b2)/4a��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
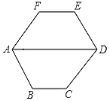
����Ŀ����ͼ��������ABCDEF���ڽǶ���ȣ���FAD��60����
��1�����ADE�Ķ�����
��2����֤��EF��BC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ɽ�����г�Խ��Խ����ѧ����ϲ����һ���꾭Ӫ��һ���ͺ�ɽ�����г�������һ�·����۶�Ϊ30000Ԫ�����·�ÿ�����ۼ۱�һ�·�ÿ�����ۼ۽���100Ԫ�������۵���������һ�����۵�������ͬ�������۶���27000Ԫ��
��1������·�ÿ�����ۼ��Ƕ���Ԫ��
��2��Ϊ�˴��������·�ÿ�����ۼ۱ȶ��·�ÿ�����ۼ۽�����10%���ۣ������Կɻ���35%����ÿ��ɽ�����г��Ľ����Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������һ��ţ�̣�����Ϊÿ��24Ԫ���涨�ۼ۲����ڽ������ڵ��ۼ�Ϊÿ��36Ԫ��ÿ�¿�����60���г����鷢�֣�������ţ�̵��ۼ�ÿ����1Ԫ����ÿ�µ�����������10�䣬��ÿ��ţ�̽���xԪ(xΪ������)��ÿ�µ�����Ϊy�䣮
��1��д��y��x֮��ĺ�����ϵʽ���Ա���x��ȡֵ��Χ��
��2������ζ��ۣ�����ʹÿ������ţ�̵����������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABC���������ֱ���A����1��3����B����5��1����C����2����2����
��1��������ABC����y��ԳƵ���A��B��C������д����A��B��C������������ꣻ
��2�������ABC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㲹ȫ֤�����̣���ͼ��DG��BC��AC��BC��EF��AB����1=��2����֤��EF��CD

֤������DG��BC��AC��BC(��֪)
���DGB=90�㣬��ACB=90��٣� ��
���DGB=��ACB ��( )
��DG��AC ��( )
���2= ��________ �ݣ� ��
�֡�1=��2 �ޣ� ��
���1=��DCA �ߣ� ��
��EF��CD �ࣨ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ʾһ�κ���y=ax+b������������y=abx��a��b�dz�������ab��0����ͼ���ǣ�������
A. 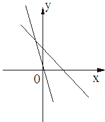 B.
B. 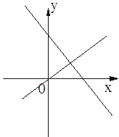
C. 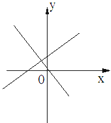 D.
D. 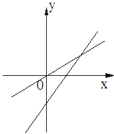
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ��ҵ����硱��ڼ䣬������ָ�����õ�����ũ�������ɵõ�����Ʒ�ۼ�13%�IJ�������������С�����һ̨A��ϴ�»���С��������һ̨B��ϴ�»�����һ���õ���������351Ԫ����֪B��ϴ�»��ۼ۱�A��ϴ�»��ۼ۶�500Ԫ����
��1��A��ϴ�»���B��ϴ�»����ۼ۸��Ƕ���Ԫ?
��2��С���С������ϴ�»�������������ʵ�ʸ��������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l���O��AB�ǡ�O��ֱ����AD��l�ڵ�D��
��1����ͼ�٣���ֱ��l���O�����ڵ�Cʱ����֤��ACƽ�֡�DAB��
��2����ͼ�ڣ���ֱ��l���O�ཻ�ڵ�E��Fʱ����֤����DAE=��BAF��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com