
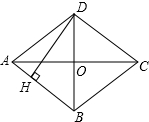
 四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB于H,求DH的长.
四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB于H,求DH的长. 分析 先根据菱形对角线互相垂直平分得:OA=$\frac{1}{2}$AC=4cm,OB=$\frac{1}{2}$BD=3cm,根据勾股定理求得AB=5cm,由菱形面积公式的两种求法列式可以求得高DH的长.
解答 解:∵四边形ABCD是菱形,AC=8cm,BD=6cm,
∴AC⊥BD,OA=$\frac{1}{2}$AC=4cm,OB=$\frac{1}{2}$BD=3cm,
∴Rt△AOB中,AB=$\sqrt{A{O}^{2}+B{O}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∵DH⊥AB,
∵菱形ABCD的面积S=$\frac{1}{2}$AC•BD=AB•DH,
$\frac{1}{2}$×6×8=5DH,
∴DH=$\frac{24}{5}$.
点评 本题考查了菱形的性质,熟练掌握菱形以下几个性质:①菱形的对角线互相垂直平分,②菱形面积=两条对角线积的一半,③菱形面积=底边×高;本题利用了面积法求菱形的高线的长.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (0,21007) | B. | ( 21007,-21007) | C. | ( 21008,-21008) | D. | ( 0,21008) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
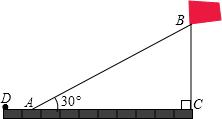 如图,小明利用升旗用的绳子测量学校旗杆BC的高度,当绳子从旗杆端垂下,地上部分还有8米,若把绳子往外拉直,绳子末端接触地面A点并与地面形成30°角,求旗杆BC的高度.
如图,小明利用升旗用的绳子测量学校旗杆BC的高度,当绳子从旗杆端垂下,地上部分还有8米,若把绳子往外拉直,绳子末端接触地面A点并与地面形成30°角,求旗杆BC的高度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9,12,14 | B. | 2,$\sqrt{2}$,$\sqrt{3}$ | C. | 4,3,$\sqrt{5}$ | D. | 4,3,5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com