Question

【题目】如图，在平面直角坐标系中， 为坐标原点，直线 ： 与直线 ： 交于点 ， 与 轴交于 ，与 轴交于点 .

（1）求 的面积；
（2）若点 在直线 上，且使得 的面积是 面积的 ，求点 的坐标.

Answer 1

【答案】
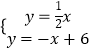（1）解：由 得：

∴A（4，2）

在y=-x+6中，当x=0，y=6，则C（0，6），S△OAC= ×6×4=12

（2）解：解：分两种情况：①如图所示，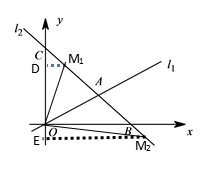

当点M1在射线AC上时，过M1作M1D⊥CO于D，则△CDM1是等腰直角三角形，
∵A（4，2），C（0，6），
∴AC= =4，
∵△OAM的面积是△OAC面积的 ，
∴AM1= AC=3 ，
∴CM1= ，
∴DM1= ，即点M1的横坐标为 ，
在直线y=﹣x+6中，当x= 时，y=6﹣ ，
∴M1（ ，6﹣ ）；
②如图所示，当点M2在射线AB上时，过M2作M2E⊥CO于E，则△CEM2是等腰直角三角形，
由题可得，AM2=AM1=3 ，
∴CM2=7 ，
∴EM2= ，即点M2的横坐标为，
在直线y=﹣x+6中，当x= 时，y=6﹣ ，
∴M2（ ，6﹣ ）．
综上所述，点M的坐标为（，6﹣ ）或（ ，6﹣ ）．


【解析】（1）先求出两直线的交点A的坐标，及直线BC与y轴的交点C的坐标，再根据三角形的面积公式，即可求出△OAC的面积。
（2）抓住已知条件中的关键词点M在直线l2上，因此分两种情况讨论：当点M1在射线AC上时，过M1作M1D⊥CO于D，则△CDM1是等腰直角三角形，易求出AC的长，再根据△OAM和△OAC的面积关系求出AM1，CM1的长，由△CDM1是等腰直角三角形，可得出DM1的长，然后结合函数解析式就可求出 点M1的坐标；当点M2在射线AB上时，过M2作M2E⊥CO于E，则△CEM2是等腰直角三角形，运用类似的方法求出点M2的坐标，即可得出结论。