
【题目】如图,在平面直角坐标系中,直线y=﹣x+3过点A(5,m)且与y轴交于点B,把点A向左平移2个单位,再向上平移4个单位,得到点C.过点C且与y=2x平行的直线交y轴于点D.
(1)求直线CD的解析式;
(2)直线AB与CD交于点E,将直线CD沿EB方向平移,平移到经过点B的位置结束,求直线CD在平移过程中与x轴交点的横坐标的取值范围.

【答案】(1)y=2x﹣4;(2)﹣![]() ≤x≤2.
≤x≤2.
【解析】
(1)将点A代入直线y=﹣x+3中,即可求出点A的坐标,通过平移即可求出点C的坐标,将CD的直线解析式设为y=2x+b,将点C代入即可求出直线CD的解析式;
(2)先求出此时直线CD与x轴的交点坐标,再根据AB的直线解析式求出点B的坐标,从而求出直线CD经过点B时的直线方程和直线CD与x轴的交点,从而可确定横坐标的取值范围.
解:(1)把A(5,m)代入y=﹣x+3得m=﹣5+3=﹣2,则A(5,﹣2),
∵点A向左平移2个单位,再向上平移4个单位,得到点C,
∴C(3,2),
∵过点C且与y=2x平行的直线交y轴于点D,
∴CD的解析式可设为y=2x+b,
把C(3,2)代入得6+b=2,解得b=﹣4,
∴直线CD的解析式为y=2x﹣4;
(2)当y=0时,2x﹣4=0,解得x=2,则直线CD与x轴的交点坐标为(2,0);
当x=0时,y=﹣x+3=3,则B(0,3),
则CD平移到经过点B时的直线解析式为y=2x+3,
当y=0时,2x+3=0,解得x=![]() ,则直线y=2x+3与x轴的交点坐标为(
,则直线y=2x+3与x轴的交点坐标为(![]() ,0),
,0),
∴直线CD在平移过程中与x轴交点的横坐标的取值范围为![]() ≤x≤2.
≤x≤2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】直线y=![]() x﹣2分别交x、y轴于C、A,物线y=﹣
x﹣2分别交x、y轴于C、A,物线y=﹣![]() x2+
x2+![]() x﹣2经过A、C两点,交x轴于另外一点B.点E为线段AC上一点,点F为线段AC延长线一点,AE=CF,点P为AC上方抛物线上的一点,当△PEF是以EF为底边的等腰三角形,且tan∠PFE=
x﹣2经过A、C两点,交x轴于另外一点B.点E为线段AC上一点,点F为线段AC延长线一点,AE=CF,点P为AC上方抛物线上的一点,当△PEF是以EF为底边的等腰三角形,且tan∠PFE=![]() 时,求点P的坐标.
时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠ABC=∠DCB,添加一个条件使△ABC≌△DCB,下列添加的条件不能使△ABC≌△DCB的是( )

A. ∠A=∠D B. AB=DC C. AC=DB D. OB=OC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() ,
,![]() .
.

![]() 用直尺和圆规作
用直尺和圆规作![]() 的平分线
的平分线![]() ,交
,交![]() 于
于![]() ,并在
,并在![]() 上取一点
上取一点![]() ,使
,使![]() ,再连接
,再连接![]() ,交
,交![]() 于
于![]() ;(要求保留作图痕迹,不必写出作法)
;(要求保留作图痕迹,不必写出作法)
![]() 依据现有条件,直接写出图中所有相似的三角形,并求出
依据现有条件,直接写出图中所有相似的三角形,并求出![]() .(图中不再增加字母和线段,不要求证明).
.(图中不再增加字母和线段,不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘在南北航线上的测量船,于A点处测得海岛B在点A的南偏东30°方向,继续向南航行30海里到达C点时,测得海岛B在C点的北偏东15°方向,那么海岛B离此航线的最近距离是( )(结果保留小数点后两位)(参考数据:![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)
A. 4.64海里 B. 5.49海里 C. 6.12海里 D. 6.21海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AC平分∠DAB,CE⊥AB于E,AB=AD+2BE,则下列结论:①AB+AD=2AE;②∠DAB+∠DCB=180°;③CD=CB;④S△ACE﹣2S△BCE=S△ADC;其中正确结论的个数是( )
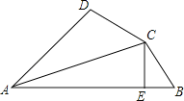
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一块直角三角板DEF放置在锐角△ABC上,使得该三角板的两条直角边DE、DF恰好分别经过点B、C.

(1)如图①,若∠A=40°时,点D在△ABC内,则∠ABC+∠ACB= 度,∠DBC+∠DCB= 度,∠ABD+∠ACD= 度;
(2)如图②,改变直角三角板DEF的位置,使点D在△ABC内,请探究∠ABD+∠ACD与∠A之间存在怎样的数量关系,并验证你的结论.
(3)如图③,改变直角三角板DEF的位置,使点D在△ABC外,且在AB边的左侧,直接写出∠ABD、∠ACD、∠A三者之间存在的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
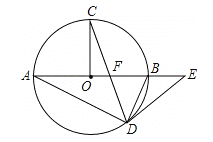
【题目】如图,在⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,在AB的延长线上有点E,且EF=ED.
(1)求证:DE是⊙O的切线;
(2)若tanA=![]() ,探究线段AB和BE之间的数量关系,并证明;
,探究线段AB和BE之间的数量关系,并证明;
(3)在(2)的条件下,若OF=1,求圆O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com