
【题目】将一块直角三角板DEF放置在锐角△ABC上,使得该三角板的两条直角边DE、DF恰好分别经过点B、C.

(1)如图①,若∠A=40°时,点D在△ABC内,则∠ABC+∠ACB= 度,∠DBC+∠DCB= 度,∠ABD+∠ACD= 度;
(2)如图②,改变直角三角板DEF的位置,使点D在△ABC内,请探究∠ABD+∠ACD与∠A之间存在怎样的数量关系,并验证你的结论.
(3)如图③,改变直角三角板DEF的位置,使点D在△ABC外,且在AB边的左侧,直接写出∠ABD、∠ACD、∠A三者之间存在的数量关系.
【答案】(1)140,90,50;(2)∠ABD+∠ACD=90°﹣∠A,证明见解析;(3)∠ACD﹣∠ABD=90°﹣∠A.
【解析】
(1)根据三角形内角和定理可得∠ABC+∠ACB=180°﹣∠A=140°,∠DBC+∠DCB=180°﹣∠DBC=90°,进而可求出∠ABD+∠ACD的度数;
(2)根据三角形内角和定义有90°+(∠ABD+∠ACD)+∠A=180°,则∠ABD+∠ACD=90°﹣∠A.
(3)设线段DC和线段AB交于点O,根据三角形外角的性质可得:∠ACD﹣∠ABD=90°﹣∠A.
(1)在△ABC中,∵∠A=40°,∴∠ABC+∠ACB=180°﹣40°=140°,
在△DBC中,∵∠BDC=90°,∴∠DBC+∠DCB=180°﹣90°=90°,∴∠ABD+∠ACD=140°﹣90°=50°.
故答案为:140,90,50.
(2)∠ABD+∠ACD与∠A之间的数量关系为:∠ABD+∠ACD=90°﹣∠A.证明如下:
在△ABC中,∠ABC+∠ACB=180°﹣∠A.
在△DBC中,∠DBC+∠DCB=90°,∴∠ABC+∠ACB﹣(∠DBC+∠DCB)=180°﹣∠A﹣90°,∴∠ABD+∠ACD=90°﹣∠A.
(3)∠ACD﹣∠ABD=90°﹣∠A.证明如下:
设线段DC和线段AB交于点O.
∵∠BOC=∠D+∠DBO=∠A+∠ACO,∴90°+∠ABD=∠A+∠ACD,∴∠ACD﹣∠ABD=90°﹣∠A.



科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.

(1)若∠A=50°,求∠DBC的度数.
(2)若AB=3,△CBD的周长为12,求△ABC得周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣x+3过点A(5,m)且与y轴交于点B,把点A向左平移2个单位,再向上平移4个单位,得到点C.过点C且与y=2x平行的直线交y轴于点D.
(1)求直线CD的解析式;
(2)直线AB与CD交于点E,将直线CD沿EB方向平移,平移到经过点B的位置结束,求直线CD在平移过程中与x轴交点的横坐标的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的个数为( )
①三角形的三条高都在三角形内,且都相交于一点
②三角形的中线都是过三角形的某一个顶点,且平分对边的直线
③在△ABC中,若![]() ,则△ABC是直角三角形
,则△ABC是直角三角形
④一个三角形的两边长分别是8和10,那么它的最短边的取值范围是2<b<18.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.

(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
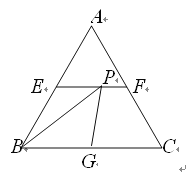
【题目】如图所示,在边长为2的正三角形ABC中,E、F、G分别为AB、
AC、BC的中点,点P为线段EF上一个动点,连接BP、GP,则△BPG的周长的最小值是
_ ▲ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,在ΔABC和ΔADE中,AB=AC,AD=AE,∠BAC=∠DAE,,且点B,A,D在同一条直线上,连接BE,CD,M,N分别为BE,CD的中点, 连接AM,AN,MN.
⑴.求证:BE=CD
⑵.求证:ΔAMN是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知坐标原点为![]() ,点
,点![]() ,将
,将![]() 绕原点
绕原点![]() 顺时针旋转
顺时针旋转![]() 后,
后,![]() 的对应点
的对应点![]() 的坐标是( )
的坐标是( )
A. (2,-1) B. (-2,1) C. (1,-2) D. (-1,2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com