练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

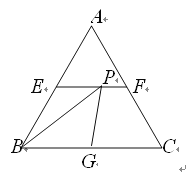
    【题目】如图所示，在边长为2的正三角形ABC中，E、F、G分别为AB、

    AC、BC的中点，点P为线段EF上一个动点，连接BP、GP，则△BPG的周长的最小值是

    _ ▲ ．

    【答案】3

    【解析】

    连接AG交EF于M，根据等边三角形的性质证明A、G关于EF对称，得到P，△PBG周长最小，求出AB+BG即可得到答案．

    解：要使△PBG的周长最小，而BG=1一定，只要使BP+PG最短即可，

    连接AG交EF于M，

    ∵等边△ABC，E、F、G分别为AB、AC、BC的中点，

    ∴AG⊥BC，EF∥BC，

    ∴AG⊥EF，AM=MG，

    ∴A、G关于EF对称，

    即当P和E重合时，此时BP+PG最小，即△PBG的周长最小，

    AP=PG，BP=BE，

    最小值是：PB+PG+BG=AE+BE+BG=AB+BG=2+1=3．

    故答案为3．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB＝AC，AD⊥BC于点D,则下列四个结论中：

    ①线段AD上任意一点到点B的距离与到点C的距离相等;

    ②线段AD上任意一点到AB的距离与到AC的距离相等;

    ③若点Q是线段AD的三等分点 ,则△ACQ的面积是△ABC面积的;

    ④若,则;

    正确结论的序号是（ ）

    A.①②③B.①②④C.①③④D.②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一艘在南北航线上的测量船，于A点处测得海岛B在点A的南偏东30°方向，继续向南航行30海里到达C点时，测得海岛B在C点的北偏东15°方向，那么海岛B离此航线的最近距离是（　　）（结果保留小数点后两位）（参考数据：≈1.732，≈1.414）

    A. 4.64海里 B. 5.49海里 C. 6.12海里 D. 6.21海里

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，ΔABC中，AD是高，AE、BF是角平分线，它们相交与点O，∠BAC=50°，∠C=70°，则∠DAC的度数为__________，∠BOA的度数为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将一块直角三角板DEF放置在锐角△ABC上，使得该三角板的两条直角边DE、DF恰好分别经过点B、C．

    （1）如图①，若∠A=40°时，点D在△ABC内，则∠ABC+∠ACB=　 　度，∠DBC+∠DCB=　 　度，∠ABD+∠ACD=　 　度；

    （2）如图②，改变直角三角板DEF的位置，使点D在△ABC内，请探究∠ABD+∠ACD与∠A之间存在怎样的数量关系，并验证你的结论．

    （3）如图③，改变直角三角板DEF的位置，使点D在△ABC外，且在AB边的左侧，直接写出∠ABD、∠ACD、∠A三者之间存在的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，MN是⊙O的直径，若∠A＝10°，∠PMQ＝40°，以PM为边作圆的内接正多边形，则这个正多边形是________边形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图∠BAC=60°，半径长1的⊙O与∠BAC的两边相切，P为⊙O上一动点，以P为圆心，PA长为半径的⊙P交射线AB、AC于D、E两点，连接DE，则线段DE长度的最大值为（　　）

    A. 3 B. 6 C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，设△ABC的两边AC与BC之和为a，M是AB的中点，MC=MA=5，则a的取值范围是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形放置在平面直角坐标系中，，所在直线为轴，所在直线为轴，反比例函数的图象经过的中点，并且与交于点，已知．则的长等于（ ）

    A. 2.5 B. 2 C. 1.5 D. 1

    查看答案和解析>>

    同步练习册答案