
【题目】如图,在△ABC中,AB=AC,AD⊥BC于点D,则下列四个结论中:
①线段AD上任意一点到点B的距离与到点C的距离相等;
②线段AD上任意一点到AB的距离与到AC的距离相等;
③若点Q是线段AD的三等分点 ,则△ACQ的面积是△ABC面积的![]() ;
;
④若![]() ,则
,则![]() ;
;
正确结论的序号是( )

A.①②③B.①②④C.①③④D.②③④
【答案】B
【解析】
先根据等腰三角形三线合一的性质得出AD是BC的中垂线,再由中垂线的性质可判断①正确;
先根据等腰三角形三线合一的性质得出AD是角平分线,根据角平分线的性质可判断②正确;
根据等腰三角形三线合一的性质得出AD是BC的中线,得到△ADC的面积=△ABC的面积的![]() ,若点Q是线段AD的三等分点,则△ACQ的面积是△ADC面积的
,若点Q是线段AD的三等分点,则△ACQ的面积是△ADC面积的![]() 或
或![]() ,进而得到△ACQ的面积是△ABC面积的
,进而得到△ACQ的面积是△ABC面积的![]() 或
或![]() ,从而可判断③错误;
,从而可判断③错误;
根据等腰三角形三线合一的性质得出AD是BC的中垂线,得出∠CAD=30°,由30°角所对直角边等于斜边的一半,即可判断④正确.
∵AB=AC,AD⊥BC,∴AD是∠BAC的平分线,BD=CD,∴线段AD上任一点到点C、点B的距离相等,∴①正确;
∵AB=AC,AD⊥BC,∴AD是∠BAC的平分线,∴AD上任意一点到AB、AC的距离相等,②正确;
∵AB=AC,AD⊥BC,∴AD是∠BAC的平分线,BD=CD,∴△ADC的面积=△ABC的面积的![]() ,若点Q是线段AD的三等分点,则△ACQ的面积是△ADC面积的
,若点Q是线段AD的三等分点,则△ACQ的面积是△ADC面积的![]() 或
或![]() ,∴△ACQ的面积是△ABC面积的
,∴△ACQ的面积是△ABC面积的![]() 或
或![]() ,∴③错误;
,∴③错误;
∵AB=AC,AD⊥BC,∴AD是∠BAC的平分线,BD=CD.
∵AB=AC,∴∠B=∠C.
∵∠B=60°,∴∠C=60°,∴∠CAD=30°,∴CD=![]() AC,∴BD=
AC,∴BD=![]() AC,∴④正确.
AC,∴④正确.
故选B.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,AD=5,E为BC上一点,BE∶CE=3∶2,连接AE,点P从点A出发,沿射线AB的方向以每秒1个单位长度的速度匀速运动,过点P作PF∥BC交直线AE于点F.
(1)线段AE=______;
(2)设点P的运动时间为t(s),EF的长度为y,求y关于t的函数关系式,并写出t的取值范围;
(3)当t为何值时,以F为圆心的⊙F恰好与直线AB、BC都相切?并求此时⊙F的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,抛物线![]() 经过点
经过点![]() 、
、![]() .
.
![]() 求
求![]() 、
、![]() 的值;
的值;
![]() 如图,点
如图,点![]() 与点
与点![]() 关于点
关于点![]() 对称,过点
对称,过点![]() 的直线交
的直线交![]() 轴于点
轴于点![]() ,交抛物线于另一点
,交抛物线于另一点![]() .若
.若![]() ,求
,求![]() 的值;
的值;
![]() 如图,在
如图,在![]() 的条件下,点
的条件下,点![]() 是
是![]() 轴上一点,连
轴上一点,连![]() 、
、![]() 分别交抛物线于点
分别交抛物线于点![]() 、
、![]() ,探究
,探究![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料并解答后面的问题:
(阅读)
小亮:你能求出x2+4x﹣3的最小值吗?如果能,其最小值是多少?
小华:能.求解过程如下:
因为x2+4x﹣3=x2+4x+4﹣4﹣3=(x2+4x+4)﹣(4+3)=(x+2)2﹣7.
而(x+22)≥0,所以x2+4x﹣3的最小值是﹣7.
(1)小华的求解过程正确吗?
(2)你能否求出x2﹣5x+4的最小值?如果能,写出你的求解过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.

(1)若∠A=50°,求∠DBC的度数.
(2)若AB=3,△CBD的周长为12,求△ABC得周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
现有甲、乙两种机器加工零件,甲种机器比乙种机器每小时多加工30个,甲种机器加工900个零件所用时间与乙种机器加工600个零件所用时间相等,求两种机器每小时各加工多少个零件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC 中,∠A=30°,∠B=90°,AC=8,点 D 在边 AB, 且 BD=![]() ,点 P 是△ABC 边上的一个动点,若 AP=2PD 时,则 PD的长是____________.
,点 P 是△ABC 边上的一个动点,若 AP=2PD 时,则 PD的长是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个多边形的所有内角与它的一个外角之和是2018°,求这个外角的度数和它的边数.
【答案】38° ; 边数13
【解析】试题分析:根据多边形的内角和公式(n-2)180°可知,多边形的内角和是180°的倍数,然后列式求解即可.
试题解析:设多边形的边数是n,加的外角为α,则
(n-2)180°+α=2018°,
α=2378°-180°n,又0<α<180°,
即0<2378°-180°n<180°,
解得: ![]() <n<
<n<![]() ,
,
又n为正整数,
可得n=13,
此时α=38°满足条件,
答:这个外角的度数是38°,它的13边形.
【点睛】本题考查了多边形的内角和公式,利用好多边形的内角和是180°的倍数是解题的关键.
【题型】解答题
【结束】
22
【题目】已知![]() , 求 (1)
, 求 (1) ![]() ; (2)
; (2) ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
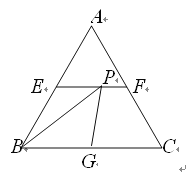
【题目】如图所示,在边长为2的正三角形ABC中,E、F、G分别为AB、
AC、BC的中点,点P为线段EF上一个动点,连接BP、GP,则△BPG的周长的最小值是
_ ▲ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com