
【题目】已知如图,抛物线![]() 经过点
经过点![]() 、
、![]() .
.
![]() 求
求![]() 、
、![]() 的值;
的值;
![]() 如图,点
如图,点![]() 与点
与点![]() 关于点
关于点![]() 对称,过点
对称,过点![]() 的直线交
的直线交![]() 轴于点
轴于点![]() ,交抛物线于另一点
,交抛物线于另一点![]() .若
.若![]() ,求
,求![]() 的值;
的值;
![]() 如图,在
如图,在![]() 的条件下,点
的条件下,点![]() 是
是![]() 轴上一点,连
轴上一点,连![]() 、
、![]() 分别交抛物线于点
分别交抛物线于点![]() 、
、![]() ,探究
,探究![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.

【答案】(1)b=-2,c=-3;(2)1;(3)见解析.
【解析】
(1)利用待定系数法即可解决问题.
(2)取点Q(1,4),P(0,1),如图1中,作QR⊥y轴于R,连接PQ,则RQ=OP=1,PR=OC=OB=3,由△POR≌△BPO≌△CAO,推出BQ与y轴的交点是N,与抛物线的交点是M,利用方程组即可解决问题.
(3)结论:EF∥BM或EF与BM重合.设P(0,m),求出直线PM、PB,再利用方程组求出点E、F坐标,求出直线EF的解析式即可解决问题.
解:![]() ∵抛物线
∵抛物线![]() 经过点
经过点![]() 、
、![]() ,
,
∴有方程组![]() ,解得
,解得![]() ,
,
∴![]() ,
,![]() .
.
![]() ∵抛物线解析式为
∵抛物线解析式为![]() ,
,

∴点![]() 坐标
坐标![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∵点![]() 与点
与点![]() 关于点
关于点![]() 对称
对称
∴![]() 是等腰直角三角形,∴
是等腰直角三角形,∴![]() ,
,
取点![]() ,
,![]() ,如图
,如图![]() 中,作
中,作![]() 轴于
轴于![]() ,连接
,连接![]() ,则
,则![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,∵
,∵![]() ,
,
∴![]() ,∵
,∵![]() ,
,
∴![]() ,
,
∴由此![]() 与
与![]() 轴的交点是
轴的交点是![]() ,与抛物线的交点是
,与抛物线的交点是![]() ,
,
∵![]() ,
,![]() ,设直线
,设直线![]() 为
为![]() ,则
,则![]() ,解得
,解得![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
∴![]() ,
,
由![]() 解得
解得![]() 或
或![]() ,
,
∵![]() ,∴
,∴![]() ,
,
作![]() 轴于
轴于![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]()
∴![]() .
.
![]() 结论:
结论:![]() 或
或![]() 与
与![]() 重合.
重合.
理由:设![]() ,
,
∵![]() ,
,![]() ,
,
∴可得直线![]() 的解析式为
的解析式为![]() ,直线
,直线![]() 的解析式为
的解析式为![]() ,
,
由 消去
消去![]() 得
得![]() ,
,![]() ,
,
∴![]() 或
或![]() ,
,![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,
,

∴方程组的解为![]() 或
或 ,
,
∴![]() ,
,
由 解得
解得![]() 或
或 ,
,
∴![]() ,
,
设直线![]() 解析式为
解析式为![]() ,
,
则 ,
,
∴![]() ,
,
∴![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
∵直线![]() 的解析式为
的解析式为![]() ,
,
∴![]() 时,
时,![]() ,
,![]() 时,直线
时,直线![]() 与
与![]() 重合.
重合.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】探究题:如图,AB⊥BC,射线CM⊥BC,且BC=5cm,AB=1cm,点P是线段BC(不与点B、C重合)上的动点,过点P作DP⊥AP交射线CM于点D,连结AD.

(1)如图1,若BP=4cm,则CD= ;
(2)如图2,若DP平分∠ADC,试猜测PB和PC的数量关系,并说明理由;
(3)若△PDC是等腰三角形,则CD= cm.(请直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某茶叶公司经销一种茶叶,每千克成本为![]() 元,市场调查发现在一段时间内,销量
元,市场调查发现在一段时间内,销量![]() (千克)随销售单价
(千克)随销售单价![]() (元/千克)的变化而变化,具有关系为:
(元/千克)的变化而变化,具有关系为:![]() ,物价部门规定每千克的利润不得超过
,物价部门规定每千克的利润不得超过![]() 元.设这种茶叶在这段时间内的销售利润
元.设这种茶叶在这段时间内的销售利润![]() (元),解答下列问题:
(元),解答下列问题:
![]() 求
求![]() 与
与![]() 的关系式;
的关系式;
![]() 当
当![]() 取何值时,
取何值时,![]() 的值最大?并求出最大值;
的值最大?并求出最大值;
![]() 当销售利润
当销售利润![]() 的值最大时,销售额也是最大吗?判断并说明理由.
的值最大时,销售额也是最大吗?判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个关于![]() 的代数式
的代数式![]() ,若存在一个系数为正数关于
,若存在一个系数为正数关于![]() 的单项式
的单项式![]() ,使
,使![]() 的结果是所有系数均为整数的整式,则称单项式
的结果是所有系数均为整数的整式,则称单项式![]() 为代数式
为代数式![]() 的“整系单项式” ,例如:
的“整系单项式” ,例如:
当![]() 时,由于
时,由于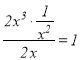 ,故
,故![]() 是
是![]() 的整系单项式;
的整系单项式;
当![]() 时,由于
时,由于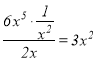 ,故
,故![]() 是
是![]() 的整系单项式;
的整系单项式;
当![]() 时,由于
时,由于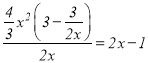 ,故
,故![]() 是
是![]() 的整系单项式;
的整系单项式;
当![]() 时,由于
时,由于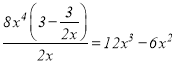 ,故
,故![]() 是
是![]() 的整系单项式;
的整系单项式;
显然,当代数式![]() 存在整系单项式
存在整系单项式![]() 时,
时,![]() 有无数个,现把次数最低,系数最小的整系单项式
有无数个,现把次数最低,系数最小的整系单项式![]() 记为
记为![]() ,例如:
,例如:![]() .
.
阅读以上材料并解决下列问题:
⑴.判断:当![]() 时,
时,![]()
![]() 的整系单项式(填“是”或“不是”);
的整系单项式(填“是”或“不是”);
⑵.当![]() 时,
时,![]() = ;
= ;
⑶.解方程: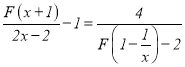 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD⊥BC于点D,则下列四个结论中:
①线段AD上任意一点到点B的距离与到点C的距离相等;
②线段AD上任意一点到AB的距离与到AC的距离相等;
③若点Q是线段AD的三等分点 ,则△ACQ的面积是△ABC面积的![]() ;
;
④若![]() ,则
,则![]() ;
;
正确结论的序号是( )

A.①②③B.①②④C.①③④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘在南北航线上的测量船,于A点处测得海岛B在点A的南偏东30°方向,继续向南航行30海里到达C点时,测得海岛B在C点的北偏东15°方向,那么海岛B离此航线的最近距离是( )(结果保留小数点后两位)(参考数据:![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)
A. 4.64海里 B. 5.49海里 C. 6.12海里 D. 6.21海里
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com