
【题目】已知二次函数y=x2-2x-3与x轴交于A、B两点,在x轴上方的抛物线上有一点C,且△ABC的面积等于10,则C点坐标为________.
【答案】(4,5)或(-2,5)
【解析】
根据二次函数y=x2-2x-3与x轴交于A、B两点,可以求得A、B两点的坐标,由在抛物线上有一点C,使得△ABC的面积等于10,可以设出点C的坐标,从而可以求得点C的坐标.
将y=0代入y=x2-2x-3可得,0=x2-2x-3,
解得x1=-1,x2=3.
∵二次函数y=x2-2x-3与x轴交于A、B两点,
∴点A的坐标为(-1,0),点B的坐标为(3,0).
∵点C在二次函数y=x2-2x-3上,设点C的坐标为(x,x2-2x-3),
又∵△ABC的面积等于10,
∴10=![]() .
.
解得x1=-2,x2=4.
故点C的坐标为:(-2,5)或(4,5).
故答案为(4,5)或(-2,5)


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求,商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价150元销售,最后剩下50件按八折优惠卖出,求两批衬衫全部售完后利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,点D是线段AC上的一动点,E在BC的延长线上,且BD=DE.
(1)如图1,若点D为线段AC的中点,求证:AD=CE;
(2)如图2,若点D为线段AC上任意一点,试确定线段AD与CE的大小关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象交x轴于A(﹣1,0)、B(2,0)两点,交y轴于点C(0,﹣2),过点A、C画直线.
(1)求二次函数的解析式;
(2)若点P在x轴正半轴上,且PA=PC,求OP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠B=60°,D、E分别为AB、BC上的点,且AE、CD交于点F.若AE、CD为△ABC的角平分线.
(1)求证:∠AFC=120°;
(2)若AD=6,CE=4,求AC的长?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两数学兴趣小组测量山CD 的高度. 甲小组在地面A处测量,乙小组在上坡B处测量,AB=200 m. 甲小组测得山顶D的仰角为45°,山坡B处的仰角为30°;乙小组测得山顶D 的仰角为58°. 求山CD的高度(结果保留一位小数).参考数据:![]() ,
,![]() ,供选用.
,供选用.

查看答案和解析>>
科目:初中数学 来源: 题型:
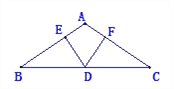
【题目】在△ABC中,AB=AC,D是BC的中点,DE⊥AB, DF⊥AC,垂足分别是E,F.
(1)证明:DE=DF;
(2)只添加一个条件,使四边形EDFA是正方形.并证明结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com