
【题目】已知:如图,在△ABC中,∠B=60°,D、E分别为AB、BC上的点,且AE、CD交于点F.若AE、CD为△ABC的角平分线.
(1)求证:∠AFC=120°;
(2)若AD=6,CE=4,求AC的长?

【答案】(1)证明见解析;(2)AC=10.
【解析】
(1)由题意∠BAC+∠BCA=120°,根据∠AFC=180﹣∠FAC﹣∠FCA=180﹣![]() =120°,即可解决问题;(2)在AC上截取AG=AD=6,连接FG.只要证明△ADF≌△AGF(SAS),推出∠AFD=∠AFG=60°,∠GFC=∠CFE=60°,再证明△CGF≌△CEF(ASA),推出CG=CE=4,由此即可解决问题.
=120°,即可解决问题;(2)在AC上截取AG=AD=6,连接FG.只要证明△ADF≌△AGF(SAS),推出∠AFD=∠AFG=60°,∠GFC=∠CFE=60°,再证明△CGF≌△CEF(ASA),推出CG=CE=4,由此即可解决问题.
(1)∵AE、CD分别为△ABC的角平分线,
∴∠FAC=![]() ,∠FCA=
,∠FCA=![]() ,
,
∵∠B=60°
∴∠BAC+∠BCA=120°,
∴∠AFC=180﹣∠FAC﹣∠FCA=180°﹣![]() ×120°=120°.
×120°=120°.
(2)在AC上截取AG=AD=6,连接FG.
∵AE、CD分别为△ABC的角平分线
∴∠FAC=∠FAD,∠FCA=∠FCE,
∵∠AFC=120°,
∴∠AFD=∠CFE=60°,
在△ADF和△AGF中
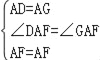 ,
,
∴△ADF≌△AGF(SAS)
∴∠AFD=∠AFG=60°,
∴∠GFC=∠CFE=60°,
在△CGF和△CEF中
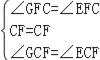 ,
,
∴△CGF≌△CEF(ASA),
∴CG=CE=4,
∴AC=10.


科目:初中数学 来源: 题型:
【题目】有下列说法:![]() 形状相同的图形是全等形;
形状相同的图形是全等形;![]() 全等形的大小相同,形状也相同;
全等形的大小相同,形状也相同;![]() 全等三角形的面积相等;
全等三角形的面积相等;![]() 面积相等的两个三角形全等;
面积相等的两个三角形全等;![]() 若
若![]() ≌
≌![]() ,
,![]() ≌
≌![]() ,则
,则![]() ≌
≌![]() 其中正确的说法有
其中正确的说法有![]()
![]()
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】襄阳市某企业积极响应政府“创新发展”的号召,研发了一种新产品.已知研发、生产这种产品的成本为30元/件,且年销售量y(万件)关于售价x(元/件)的函数解析式为:y= ![]() .
.
(1)若企业销售该产品获得的年利润为W(万元),请直接写出年利润W(万元)关于售价x(元/件)的函数解析式;
(2)当该产品的售价x(元/件)为多少时,企业销售该产品获得的年利润最大?最大年利润是多少?
(3)若企业销售该产品的年利润不少于750万元,试确定该产品的售价x(元/件)的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某运算程序,该程序是循环迭代的一种.根据该程序的指令,如果输入![]() 的值是10,那么得到第1次输出的值是5;把第1次输出的值再次输入,那么第2次输出的值是6;把第2次输出的值再次输入,那么第3次输出的值是3;…,第2018次输出的值是( )
的值是10,那么得到第1次输出的值是5;把第1次输出的值再次输入,那么第2次输出的值是6;把第2次输出的值再次输入,那么第3次输出的值是3;…,第2018次输出的值是( )

A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC 中,AB=AC,∠BAC=90°,D 是BC 上一点,EC⊥BC,EC=BD,DF=FE.
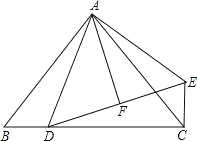
求证:(1)△ABD≌△ACE;
(2)AF⊥DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处用测角仪测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.请根据这些数据求出河的宽度为米.(结果保留根号)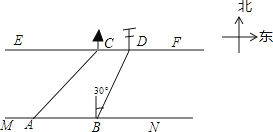
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现计划把甲种货物1240吨和乙种货物880吨用一列货车运往某地,已知这列货车挂有A、B两种不同规格的货车车厢共40节,使用A型车厢每节费用为6000元,使用B型车厢每节费用为8000元。
(1)设运送这批货物的总费用为![]() 万元,这列货车挂A型车厢
万元,这列货车挂A型车厢![]() 节,试写出
节,试写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果每节A型车厢最多可装甲种货物35吨和乙种货物15吨,每节B型车厢最多可装甲种货物25吨和乙种货物35吨,装货时按此要求安排A、B两种车厢的节数,那么共有哪几种安排车厢的方案?
(3)在上述方案中,哪种方案运费最省,最少运费为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AB为半圆O的直径,D为BA的延长线上一点,DC为半圆O的切线,切点为C.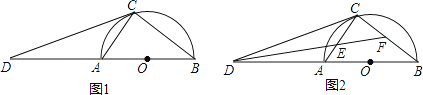
(1)求证:∠ACD=∠B;
(2)如图2,∠BDC的平分线分别交AC,BC于点E,F;
①求tan∠CFE的值;
②若AC=3,BC=4,求CE的长.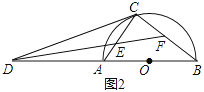
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com