
【题目】如图1,AB为半圆O的直径,D为BA的延长线上一点,DC为半圆O的切线,切点为C.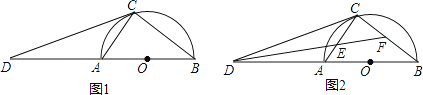
(1)求证:∠ACD=∠B;
(2)如图2,∠BDC的平分线分别交AC,BC于点E,F;
①求tan∠CFE的值;
②若AC=3,BC=4,求CE的长.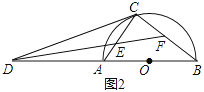
【答案】
(1)
证明:如图1中 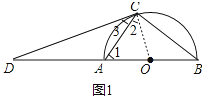 ,连接OC.
,连接OC.
∵OA=OC,
∴∠1=∠2,
∵CD是⊙O切线,
∴OC⊥CD,
∴∠DCO=90°,
∴∠3+∠2=90°,
∵AB是直径,
∴∠1+∠B=90°,
∴∠3=∠B
(2)
解:①∵∠CEF=∠ECD+∠CDE,∠CFE=∠B+∠FDB,
∵∠CDE=∠FDB,∠ECD=∠B,
∴∠CEF=∠CFE,∵∠ECF=90°,
∴∠CEF=∠CFE=45°,
∴tan∠CFE=tan45°=1.
②在RT△ABC中,∵AC=3,BC=4,
∴AB= ![]() =5,
=5,
∵∠CDA=∠BDC,∠DCA=∠B,
∴△DCA∽△DBC,
∴ ![]() =
= ![]() =
= ![]() ,设DC=3k,DB=4k,
,设DC=3k,DB=4k,
∵CD2=DADB,
∴9k2=(4k﹣5)4k,
∴k= ![]() ,
,
∴CD= ![]() ,DB=
,DB= ![]() ,
,
∵∠CDE=∠BDF,∠DCE=∠B,
∴△DCE∽△DBF,
∴ ![]() ,设EC=CF=x,
,设EC=CF=x,
∴ 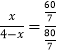 ,
,
∴x= ![]() .
.
∴CE= ![]()
【解析】(1)利用等角的余角相等即可证明.
(2)①只要证明∠CEF=∠CFE即可.②由△DCA∽△DBC,得 ![]() =
= ![]() =
= ![]() =
= ![]() ,设DC=3k,DB=4k,由CD2=DADB,得9k2=(4k﹣5)4k,由此求出DC,DB,再由△DCE∽△DBF,得
,设DC=3k,DB=4k,由CD2=DADB,得9k2=(4k﹣5)4k,由此求出DC,DB,再由△DCE∽△DBF,得 ![]() =
= ![]() ,设EC=CF=x,列出方程即可解决问题.本题考查切线的性质、相似三角形的判定和性质、勾股定理等知识,解题的关键是正确寻找相似三角形,利用相似三角形的性质解决问题,学会用方程的思想思考问题,属于中考常考题型.
,设EC=CF=x,列出方程即可解决问题.本题考查切线的性质、相似三角形的判定和性质、勾股定理等知识,解题的关键是正确寻找相似三角形,利用相似三角形的性质解决问题,学会用方程的思想思考问题,属于中考常考题型.


科目:初中数学 来源: 题型:
【题目】按要求完成下列题目.
![]() 求:
求:![]() 的值.
的值.
对于这个问题,可能有的同学接触过,一般方法是考虑其中的一般项,注意到上面和式的每一项可以写成![]() 的形式,而
的形式,而![]() ,这样就把
,这样就把![]() 一项
一项![]() 分
分![]() 裂成了两项.
裂成了两项.
试着把上面和式的每一项都裂成两项,注意观察其中的规律,求出上面的和,并直接写出![]() 的值.
的值.
![]() 若
若![]()
![]() 求:A、B的值:
求:A、B的值:
![]() 求:
求:![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠B=60°,D、E分别为AB、BC上的点,且AE、CD交于点F.若AE、CD为△ABC的角平分线.
(1)求证:∠AFC=120°;
(2)若AD=6,CE=4,求AC的长?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高科技创新意识,我市某中学在“2016年科技节”活动中举行科技比赛,包括“航模”、“机器人”、“环保”、“建模”四个类别(每个学生只能参加一个类别的比赛),各类别参赛人数统计如图:
请根据以上信息,解答下列问题:
(1)全体参赛的学生共有人,“建模”在扇形统计图中的圆心角是°;
(2)将条形统计图补充完整;
(3)在比赛结果中,获得“环保”类一等奖的学生为1名男生和2名女生,获得“建模”类一等奖的学生为1名男生和1名女生,现从这两类获得一等奖的学生中各随机选取1名学生参加市级“环保建模”考察活动,问选取的两人中恰为1男生1女生的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE:EC=2:1,则线段CH的长是( )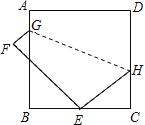
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实施素质教育以来,某中学立足于学生的终身发展,大力开发课程资源,在七年级设立六个课外学习小组,下面是七年级学生参加六个学习小组的统计表和扇形统计图,请你根据图表中提供的信息回答下列问题.
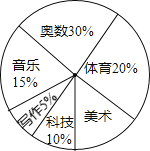
学习小组 | 体育 | 美术 | 科技 | 音乐 | 写作 | 奥数 |
人数 | 72 | 36 | 54 | 18 |
(1)七年级共有学生 人;
(2)在表格中的空格处填上相应的数字;
(3)表格中所提供的六个数据的中位数是 ;
(4)众数是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com