
【题目】如图,△ABC是等边三角形,点D是线段AC上的一动点,E在BC的延长线上,且BD=DE.
(1)如图1,若点D为线段AC的中点,求证:AD=CE;
(2)如图2,若点D为线段AC上任意一点,试确定线段AD与CE的大小关系,并说明理由.

【答案】(1)详见解析;(2)AD=CE,理由详见解析.
【解析】
(1)根据等边三角形三线合一的性质即可求得∠DBC的度数,再根据BD=DE可求得∠E的度数,进而可求得∠CDE的度数,于是可判断CD与CE的关系,进一步即可得出结论;
(2)作DF∥AB,利用AAS可证△BDF≌△EDC,得BF=CE,再证AD=BF即可,而易证△DCF是等边三角形,所以CF=CD,再根据CA=CB,问题即得解决.
解:(1)∵△ABC是等边三角形,点D为线段AC的中点,
∴BD平分∠ABC,∠ABC=∠ACB=60°,∴∠DBE=30°,
∵BD=DE,∴∠E=∠DBE=30°,
∵∠DCE=180°﹣∠ACB=120°,
∴∠CDE=180°﹣120°﹣30°=30°,即∠E=∠CDE,
∴CD=CE,
∴AD=CE;
(2)作DF∥AB交BC于点F,如图2,
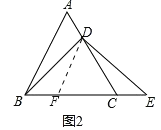
∵DF∥AB,∴∠DFC=∠ABC=60°,∠FDC=∠A=60°,
∴△DCF是等边三角形,
∴CF=CD,∵CA=CB,∴BF=AD,
∵∠DFC=60°,∴∠BFD=120°,
∵∠ACB=60°,∴∠ACE=120°,
∴∠BFD=∠ECD,
∵BD=DE,∴∠E=∠DBE,
在△BDF和△EDC中,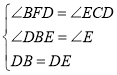 ,
,
∴△BDF≌△EDC(AAS),
∴BF=CE,
∴AD=CE.


科目:初中数学 来源: 题型:
【题目】(10分)如图①,将两块全等的三角板拼在一起,其中△ABC的边BC在直线l上,AC⊥BC且AC = BC;△EFP的边FP也在直线l上,边EF与边AC重合,EF⊥FP且EF = FP。
(1)在图①中,请你通过观察、测量,猜想并写出AB与AP所满足的数量关系和位置关系;
(2)将三角板△EFP沿直线l向左平移到图②的位置时,EP交AC于点Q,连接AP、BQ。猜想并写出BQ与AP所满足的数量关系和位置关系,并证明你的猜想;
(3)将三角板△EFP沿直线l向左平移到图③的位置时,EP的延长线交AC的延长线于点Q,连接AP、BQ。你认为(2)中猜想的BQ与AP所满足的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.
请根据图表信息回答下列问题:
视力 | 频数(人) | 频率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |
(1)本次调查的样本为________,样本容量为_______;
(2)在频数分布表中,a=______,b=______,并将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,根据上述信息估计全区初中毕业生中视力正常的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,我们在“格点”直角坐标系上可以看到:要找![]() 或
或![]() 的长度,可以转化为求
的长度,可以转化为求![]() 或
或![]() 的斜边长.
的斜边长.

例如:从坐标系中发现:![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,所以由勾股定理可得:
,所以由勾股定理可得:![]() .
.
(1)在图①中请用上面的方法求线段![]() 的长:
的长:![]() ______;在图②中:设
______;在图②中:设![]() ,
,![]() ,试用
,试用![]() ,
,![]() ,
,![]() ,
,![]() 表示:
表示:![]() ______.
______.
(2)试用(1)中得出的结论解决如下题目:已知:![]() ,
,![]() ,
,![]() 为
为![]() 轴上的点,且使得
轴上的点,且使得![]() 为等腰三角形,请求出
为等腰三角形,请求出![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形的周长为32cm,一个内角的度数是60°,则两条对角线的长分别是( )
A. 8cm和4![]() cm B. 4cm和8
cm B. 4cm和8![]() cm C. 8cm和8
cm C. 8cm和8![]() cm D. 4cm和4
cm D. 4cm和4![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
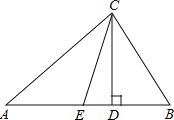
【题目】如图,在△ABC中,CD、CE分别是△ABC的高和角平分线.
(1)若∠A=30°,∠B=50°,求∠ECD的度数;
(2)试用含有∠A、∠B的代数式表示∠ECD(不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】食品加工是一种专业技术,就是把原料经过人为处理形成一种新形式的可直接食用的产品,这个过程就是食品加工.比如用小麦经过碾磨、筛选、加料搅拌、成型烘干,成为饼干,就是属于食品加工的过程.下表给出了甲、乙、丙三种原料中的维生素A、B的含量(单位:g/kg).
原料甲 | 原料乙 | 原料丙 | |
维生素A的含量 | 4 | 6 | 4 |
维生素B的含量 | 8 | 2 | 4 |
将甲、乙、丙三种原料共100kg混合制成一种新食品,其中原料甲xkg,原料乙ykg.
(1)这种新食品中,原料丙的含量__________kg,维生素B的含量__________g;(用含![]() 、
、![]() 的式子表示)
的式子表示)
(2)若这种新食品中,维生素A的含量至少为440g,维生素B的含量至少为480g,请你证明:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
(1)请在图中确定该圆弧所在圆心D点的位置,D点坐标为 ;
(2)连接AD、CD,求⊙D的半径及扇形DAC的圆心角度数;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com