Question

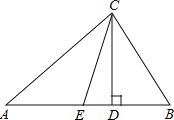
【题目】如图，在△ABC中，CD、CE分别是△ABC的高和角平分线．

（1）若∠A=30°，∠B=50°，求∠ECD的度数；

（2）试用含有∠A、∠B的代数式表示∠ECD（不必证明）

Answer 1

【答案】见解析

【解析】试题分析：（1）利用高的定义和互余得到∠BCD=90°-∠B，再根据角平分线定义得到∠BCE=∠ACB，接着根据三角形内角和定理得到∠ACB=180°-∠A-∠B，于是得到∠BCE=90°-（∠A+∠B），然后计算∠BCE-∠BCD得到∠ECD=（∠B-∠A），再把∠A=30°，∠B=50°代入计算即可；
（2）直接由（1）得到结论．

试题解析：（1）∵CD为高，∴∠CDB=90°，

∴∠BCD=90°-∠B，∵CE为角平分线，

∴∠BCE=∠ACB，而∠ACB=180°-∠A-∠B，

∴∠BCE=（180°-∠A-∠B）=90°-（∠A+∠B），

∴∠ECD=∠BCE-∠BCD =90°-（∠A+∠B）-（90°-∠B）=（∠B-∠A），

当∠A=30°，∠B=50°时，∠ECD=×（50°-30°）=10°；

（2）由（1）得∠ECD=（∠B-∠A）．