
【题目】某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.
请根据图表信息回答下列问题:
视力 | 频数(人) | 频率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |
(1)本次调查的样本为________,样本容量为_______;
(2)在频数分布表中,a=______,b=______,并将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,根据上述信息估计全区初中毕业生中视力正常的学生有多少人?

【答案】 200名初中毕业生的视力情况 200 60 0.05
【解析】
(1)用第1组的频数除以它所占的百分比即可得到样本容量,然后根据样本的定义写出样本;
(2)用样本容量乘以0.3得到a的值,用10除以10得到b的值;
(3)用样本值后面三组的频率和乘以5000可估计全区初中毕业生中视力正常的学生数.
(1)20÷0.1=200(人),
所以本次调查的样本为200名初中毕业生的视力情况,样本容量为200;
(2)a=200×0.3=60,b=10÷200=0.05;
如图,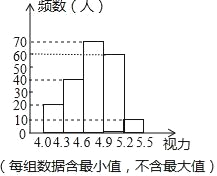
故答案为 200名初中毕业生的视力情况,200;60,0.05;
(3)5000×(0.35+0.3+0.05)=3500(人),
估计全区初中毕业生中视力正常的学生有3500人.


科目:初中数学 来源: 题型:
【题目】如图,已知线段AB,请按要求完成下列问题.
(1)用直尺和圆规作图,延长线段AB到点C,使BC=AB;反向延长线段AB到点D,使AD=AC;
(2)如果AB=2cm;
①求CD的长度;
②设点P是线段BD的中点,求线段CP的长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝“元旦”,光明学校统一组织合唱比赛,七、八年级共92人(其中七年级的人数多于八年级的人数,且七年级的人数不足90人)准备统一购买服装参加比赛.下面是某服装厂给出服装的价格表:
购买服装的套数 | 1套至45套 | 46套至90套 | 91套以上(含91套) |
每套服装的价格 | 60元 | 50元 | 40元 |
购买服装的套数 | 1套至45套 | 46套至90套 | 91套以上(含91套) |
每套服装的价格 | 60元 | 50元 | 40元 |
(1)如果两个年级分别单独购买服装一共应付5000元,求七、八年级各有多少学生参加合唱比赛;
(2)如果七年级参加合唱比赛的学生中,有10名同学抽调去参加绘画比赛,不能参加合唱比赛,请你为两个年级设计一种最省钱的购买服装方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80 m,DE=10 m,求障碍物B,C两点间的距离.(结果精确到0.1 m)(参考数据: ![]() ≈1.414,、
≈1.414,、![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上,点A和点B分别位于原点O两侧,AB=14,点A对应的数为a,点B对应的数为b.
(1) 若b=-4,则a的值为__________.
(2) 若OA=3OB,求a的值.
(3) 点C为数轴上一点,对应的数为c.若O为AC的中点,OB=3BC,直接写出所有满足条件的c的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD平分∠BAC,CE∥AD且CE=AD.
(1)求证:四边形ADCE是矩形;
(2)若△ABC是边长为![]() 的等边三角形,AC,DE相交于点O,在CE上截取CF=CO,连接OF,求线段FC的长及四边形AOFE的面积.
的等边三角形,AC,DE相交于点O,在CE上截取CF=CO,连接OF,求线段FC的长及四边形AOFE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,∠ABC=∠ACB,D为射线CB上一点(不与C、B重合),点E为射线CA上一点,∠ADE=∠AED.设∠BAD=α,∠CDE=β.
(1)如图(1),
①若∠BAC=40°,∠DAE=30°,则α= ,β= .
②写出α与β的数量关系,并说明理由;
(2)如图(2),当D点在BC边上,E点在CA的延长线上时,其它条件不变,写出α与β的数量关系,并说明理由.
(3)如图(3),D在CB的延长线上,根据已知补全图形,并直接写出α与β的关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于点O,∠AOC=48°,∠DOE∶∠BOE=5∶3,OF平分∠AOE.
(1)求∠BOE的度数;
(2)求∠DOF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【探究证明】
(1)在矩形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H.,求证:![]() ;
;
【结论应用】
(2)如图2,在满足(1)的条件下,又AM⊥BN,点M,N分别在边BC,CD上.若![]() ,求
,求![]() ;
;
【联系拓展】
(3)如图3,四边形ABCD中,∠ABC=90°,AB=AD=10,BC=CD=5,AM⊥DN,点M,N分别在边BC,AB上,求![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com