
【题目】如图,甲、乙两数学兴趣小组测量山CD 的高度. 甲小组在地面A处测量,乙小组在上坡B处测量,AB=200 m. 甲小组测得山顶D的仰角为45°,山坡B处的仰角为30°;乙小组测得山顶D 的仰角为58°. 求山CD的高度(结果保留一位小数).参考数据:![]() ,
,![]() ,供选用.
,供选用.

【答案】山高约为295.2 m.
【解析】
在Rt△AFB中,根据AB=200米,∠BAF=30°,求出BF、AF的长度,然后证明四边形BFCE是矩形,设BE=x米,在Rt△BDE中,用x表示出DE的长度,然后根据AC=DC,代入求出x的值,继而可求得山高.
过B作BF⊥AC于F,
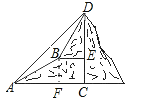
在Rt△AFB中,
∵AB=200米,∠BAF=30°,
∴BF=![]() AB=
AB=![]() ×200=100(米),
×200=100(米),
AF=ABcos30°=100![]() (米),
(米),
∵BF⊥AC,BE⊥DC,
∴四边形BFCE是矩形,
∴EC=BF=100米,
设BE=x米,则FC=x米,
在Rt△DBE中,
∵∠DBE=58°,
∴DE=tan58°BE=1.6x(米),
∵∠DAC=45°,∠C=90°,
∴∠ADC=45°,
∴AC=DC,
∵AC=AF+FC=(100![]() +x)米,
+x)米,
DC=DE+EC=(1.6x+100)米,
解得:x=122,
∴DC=DE+EC=1.6×122+100=295.2(米);
答:山的高度BC约为295.2米.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图①,我们在“格点”直角坐标系上可以看到:要找![]() 或
或![]() 的长度,可以转化为求
的长度,可以转化为求![]() 或
或![]() 的斜边长.
的斜边长.

例如:从坐标系中发现:![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,所以由勾股定理可得:
,所以由勾股定理可得:![]() .
.
(1)在图①中请用上面的方法求线段![]() 的长:
的长:![]() ______;在图②中:设
______;在图②中:设![]() ,
,![]() ,试用
,试用![]() ,
,![]() ,
,![]() ,
,![]() 表示:
表示:![]() ______.
______.
(2)试用(1)中得出的结论解决如下题目:已知:![]() ,
,![]() ,
,![]() 为
为![]() 轴上的点,且使得
轴上的点,且使得![]() 为等腰三角形,请求出
为等腰三角形,请求出![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若经过一个三角形某一顶点的一条直线可把它分成两个小等腰三角形,那么我们称这个三角形为过该顶点的生成三角形.

(1)如图,在△ABC中,∠A=90°,∠B=67.5°,请问是否是生成三角形?请你说明理由;
(2)若△ABC是等腰三角形过顶点B的生成三角形,∠C是其最小的内角,且BC是等腰三角形的底边,请探求∠ABC与∠C之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板中的两块直角板中的两个直角顶点重合在一起,即按如图所示的方式叠放在一起,其中∠A=60°,∠B=30,∠D=45°.
(1)若∠BCD=45°,求∠ACE的度数.
(2)若∠ACE=150°,求∠BCD的度数.
(3)由(1)、(2)猜想∠ACE与∠BCD存在什么样的数量关系并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
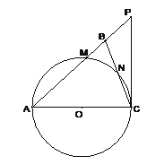
【题目】如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.
(1)求证:直线CP是⊙O的切线;
(2)若BC=2![]() ,sin∠BCP=
,sin∠BCP=![]() ,求⊙O的半径及△ACP的周长.
,求⊙O的半径及△ACP的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
(1)请在图中确定该圆弧所在圆心D点的位置,D点坐标为 ;
(2)连接AD、CD,求⊙D的半径及扇形DAC的圆心角度数;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点O为坐标原点,点A(3a,2a)在第一象限,过点A向x轴作垂线,垂足为点B,连接OA,S△AOB=12,点M从O出发,沿y轴的正半轴以每秒2个单位长度的速度运动,点N从点B出发以每秒3个单位长度的速度向x轴负方向运动,点M与点N同时出发,设点M的运动时间为t秒,连接AM,AN,MN.
(1)求a的值;
(2)当0<t<2时,
①请探究∠ANM,∠OMN,∠BAN之间的数量关系,并说明理由;
②试判断四边形AMON的面积是否变化?若不变化,请求出其值;若变化,请说明理由。
(3)当OM=ON时,请求出t的值。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台“走基层”栏目的一位记者乘汽车赴360km外的农村采访,全程的前一部分为高速公路,后一部分为乡村公路.若汽车在高速公路和乡村公路上分别以某一速度匀速行驶,汽车行驶的路程y(单位:km)与时间x(单位:h)之间的关系如图所示,则下列结论正确的是【 】
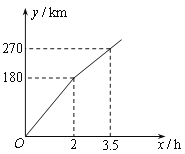
(A)汽车在高速公路上的行驶速度为100km/h
(B)乡村公路总长为90km
(C)汽车在乡村公路上的行驶速度为60km/h
(D)该记者在出发后4.5h到达采访地
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com