
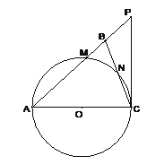
【题目】如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.
(1)求证:直线CP是⊙O的切线;
(2)若BC=2![]() ,sin∠BCP=
,sin∠BCP=![]() ,求⊙O的半径及△ACP的周长.
,求⊙O的半径及△ACP的周长.
【答案】(1)证明见解析;(2)20.
【解析】
(1)欲证明直线CP是⊙O的切线,只需证得CP⊥AC;
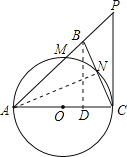
(2)利用正弦三角函数的定义求得⊙O的直径AC=5,则⊙O的半径为![]() .如图,过点B作BD⊥AC于点D,构建相似三角形:△CAN∽△CBD,所以根据相似三角形的对应边成比例求得线段BD=4;然后在直角△BCD中,利用勾股定理可以求得CD=2,所以利用平行线分线段成比例分别求得线段PC、PB的长度.则△ACP的周长迎刃可解了.
.如图,过点B作BD⊥AC于点D,构建相似三角形:△CAN∽△CBD,所以根据相似三角形的对应边成比例求得线段BD=4;然后在直角△BCD中,利用勾股定理可以求得CD=2,所以利用平行线分线段成比例分别求得线段PC、PB的长度.则△ACP的周长迎刃可解了.
(1)证明:连接AN,
∵∠ABC=∠ACB,∴AB=AC,
∵AC是⊙O的直径,∴AN⊥BC,
∴∠CAN=∠BAN,BN=CN,
∵∠CAB=2∠BCP,
∴∠CAN=∠BCP.
∵∠CAN+∠ACN=90°,
∴∠BCP+∠ACN=90°,
∴CP⊥AC
∵OC是⊙O的半径
∴CP是⊙O的切线;
(2)∵∠ANC=90°,sin∠BCP=![]() ,
,
∴![]() =
=![]() ,
,
∴AC=5,
∴⊙O的半径为![]() .
.
如图,过点B作BD⊥AC于点D.
由(1)得BN=CN=![]() BC=
BC=![]() ,
,
在Rt△CAN中,AN=![]() ,
,
在△CAN和△CBD中,
∠ANC=∠BDC=90°,∠ACN=∠BCD,
∴△CAN∽△CBD,
∴![]() ,
,
∴BD=4.
在Rt△BCD中,CD=![]() ,
,
∴AD=AC-CD=5-2=3,
∵BD∥CP,
∴![]() ,
,![]() ,
,
∴CP=![]() ,BP=
,BP=![]()
∴△APC的周长是AC+PC+AP=20.


科目:初中数学 来源: 题型:
【题目】如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于![]() BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( )
BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( )

A. 90°B. 95°C. 100°D. 105°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两数学兴趣小组测量山CD 的高度. 甲小组在地面A处测量,乙小组在上坡B处测量,AB=200 m. 甲小组测得山顶D的仰角为45°,山坡B处的仰角为30°;乙小组测得山顶D 的仰角为58°. 求山CD的高度(结果保留一位小数).参考数据:![]() ,
,![]() ,供选用.
,供选用.

查看答案和解析>>
科目:初中数学 来源: 题型:
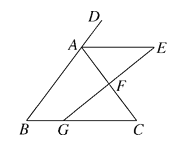
【题目】如图,在△ABC中,已知点D在线段AB的反向延长线上,过AC的中点F作线段GE交∠DAC的平分线于E,交BC于G,且AE∥BC.
(1)求证:△ABC是等腰三角形;
(2)若AE=8,AB=10,GC=2BG,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,… 组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒![]() 个单位长度,则第2019秒时,点P的坐标是________________
个单位长度,则第2019秒时,点P的坐标是________________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山地自行车越来越受中学生的喜爱.一网店经营的一个型号山地自行车,今年一月份销售额为30000元,二月份每辆车售价比一月份每辆车售价降价100元,若销售的数量与上一月销售的数量相同,则销售额是27000元.
(1)求二月份每辆车售价是多少元?
(2)为了促销,三月份每辆车售价比二月份每辆车售价降低了10%销售,网店仍可获利35%,求每辆山地自行车的进价是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,AB=10,∠ABC=60°,以AB为直径作⊙O,边CD切⊙O于点E.
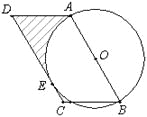
(1)圆心O到CD的距离是______;
(2)求由弧AE、线段AD、DE所围成的阴影部分的面积.(结果保留π和根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com