
【题目】在平行四边形ABCD中,AB=10,∠ABC=60°,以AB为直径作⊙O,边CD切⊙O于点E.
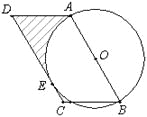
(1)圆心O到CD的距离是______;
(2)求由弧AE、线段AD、DE所围成的阴影部分的面积.(结果保留π和根号)
【答案】5;25+![]() -
- ![]() .
.
【解析】试题分析:(1)、连接OE,根据切线可得OE⊥CD,根据AB求出OE的长度,即圆心到CD的距离;(2)、根据平行四边形得出∠C=120°,∠BOE=90°,作EF∥CB,根据Rt△OEF求出OF的长度,然后得出EC和DE长度,从而求出梯形OADE的面积和扇形OAE的面积,从而得出阴影部分的面积.
试题解析:(1)、连接OE.
∵边CD切⊙O于点E.∴OE⊥CD 则OE就是圆心O到CD的距离,则圆心O到CD的距离是![]() ×AB=5.
×AB=5.
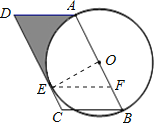
(2)∵四边形ABCD是平行四边形. ∴∠C=∠DAB=180°-∠ABC=120°,
∴∠BOE=360°-90°-60°-120°=90°, ∴∠AOE=90°,
作EF∥CB,∴∠OFE=∠ABC=60°, 在直角三角形OEF中,OE=5,
∴OF=OE![]() tan30°=
tan30°=![]() .EC=BF=5-
.EC=BF=5-![]() . 则DE=10-5+
. 则DE=10-5+![]() =5+
=5+![]() ,
,
则直角梯形OADE的面积是: ![]() (OA+DE)×OE=
(OA+DE)×OE=![]() (5+5+
(5+5+![]() )×5=25+
)×5=25+![]() .
.
扇形OAE的面积是: ![]() . 则阴影部分的面积是:25+
. 则阴影部分的面积是:25+![]() -
- ![]() .
.


 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:初中数学 来源: 题型:
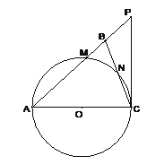
【题目】如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.
(1)求证:直线CP是⊙O的切线;
(2)若BC=2![]() ,sin∠BCP=
,sin∠BCP=![]() ,求⊙O的半径及△ACP的周长.
,求⊙O的半径及△ACP的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了拉动内需,广东启动“家电下乡”活动.某家电公司销售给农户的Ⅰ型冰箱和Ⅱ型冰箱在启动活动前一个月共售出980台,启动活动后的第一个月销售给农户的Ⅰ型和Ⅱ型冰箱的销量分别比启动活动前一个月增长30%、25%,这两种型号的冰箱共售出1254台.在启动活动前的一个月,销售给农户的Ⅰ型冰箱和Ⅱ型冰箱分别为多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果自然数m使得作竖式加法![]() 时对应的每个数位都不产生进位,则称m为“幸运数”.
时对应的每个数位都不产生进位,则称m为“幸运数”.
例如:12,321都是“幸运数”,理由是12+13+14及321+322+323每个数位都不产生进位;50,123都不是“幸运数”,理由是50+51+52及123+124+125十位或个位分别产生了进位.
(1)判断2019和2020是否是“幸运数”?请说明理由;
(2)求出三位数中小于200且是3的倍数的“幸运数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台“走基层”栏目的一位记者乘汽车赴360km外的农村采访,全程的前一部分为高速公路,后一部分为乡村公路.若汽车在高速公路和乡村公路上分别以某一速度匀速行驶,汽车行驶的路程y(单位:km)与时间x(单位:h)之间的关系如图所示,则下列结论正确的是【 】
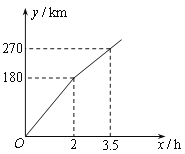
(A)汽车在高速公路上的行驶速度为100km/h
(B)乡村公路总长为90km
(C)汽车在乡村公路上的行驶速度为60km/h
(D)该记者在出发后4.5h到达采访地
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC 中,AB=AC=6cm,∠B=∠C,BC=4cm,点 D 为 AB的中点.
(1)如果点 P 在线段 BC 上以 1cm/s 的速度由点 B 向点 C 运动,同时,点 Q 在线段 CA 上由点 C 向点 A 运动.
①若点 Q 的运动速度与点 P 的运动速度相等,经过 1 秒后,△BPD 与△CQP 是否全等,请说明理由;
②若点 Q 的运动速度与点 P 的运动速度不相等,当点 Q 的运动速度为多少时,能够使△BPD 与△CQP 全等?
(2)若点 Q 以②中的运动速度从点 C 出发,点 P 以原来的运动速度从点 B 同时出发,都逆时针沿△ABC 三边运动,则经过 后,点 P 与点 Q 第一次在△ABC 的 边上相遇?(在横线上直接写出答案,不必书写解题过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,AB边上有一动点P,连接PD,线段PD绕点P顺时针旋转90°后,得到线段PE,且PE交BC于F,连接DF,过点E作EQ⊥AB的延长线于点Q.
(1)求线段PQ的长;
(2)问:点P在何处时,△PFD∽△BFP,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P,且AE=CF.
(1)求证:AF=BE,并求∠FPB的度数;
(2)若AE=2,试求AP·AF的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=AC,∠C=70°,△AB′C′与△ABC 关于直线 EF对称,∠CAF=10°,连接 BB′,则∠ABB′的度数是( )

A. 30° B. 35° C. 40° D. 45°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com