
【题目】△ABC中,BC=10,AC﹣AB=6.过C作∠BAC的角平分线的垂线,则S△BDC的最大值为( )

A.10B.15C.20D.25
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了60次实验,实验的结果如下:

(1)计算“3点朝上”的频率和“5点朝上”的频率.
(2)小颖说:“根据实验,一次实验中出现5点朝上的概率最大”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次.”小颖和小红的说法正确吗?为什么?
(3)小颖和小红各投掷一枚骰子,用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则下列结论:① △ODC是等边三角形;②BC=2AB;③∠AOE=135°; ④S△AOE=S△COE,其中正确的结论的个数有

A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为6cm,点E,M分别是线段BD,AD上的动点,连接AE并延长,交边BC于F,过M作MN⊥AF,垂足为H,交边AB于点N.
(1)如图①,若点M与点D重合,求证:AF=MN;
(2)如图②,若点M从点D出发,以1cm/s的速度沿DA向点A运动,同时点E从点B出发,以![]() cm/s的速度沿BD向点D运动,运动时间为ts.
cm/s的速度沿BD向点D运动,运动时间为ts.
①设BF=ycm,求y关于t的函数表达式;
②当BN=2AN时,连接FN,求FN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,我们在“格点”直角坐标系上可以看到:要找![]() 或
或![]() 的长度,可以转化为求
的长度,可以转化为求![]() 或
或![]() 的斜边长.
的斜边长.

例如:从坐标系中发现:![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,所以由勾股定理可得:
,所以由勾股定理可得:![]() .
.
(1)在图①中请用上面的方法求线段![]() 的长:
的长:![]() ______;在图②中:设
______;在图②中:设![]() ,
,![]() ,试用
,试用![]() ,
,![]() ,
,![]() ,
,![]() 表示:
表示:![]() ______.
______.
(2)试用(1)中得出的结论解决如下题目:已知:![]() ,
,![]() ,
,![]() 为
为![]() 轴上的点,且使得
轴上的点,且使得![]() 为等腰三角形,请求出
为等腰三角形,请求出![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点,若点D为BC边的中点,点M为线段EF上一动点,则![]() 周长的最小值为______.
周长的最小值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
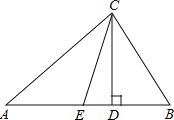
【题目】如图,在△ABC中,CD、CE分别是△ABC的高和角平分线.
(1)若∠A=30°,∠B=50°,求∠ECD的度数;
(2)试用含有∠A、∠B的代数式表示∠ECD(不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
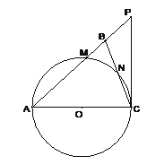
【题目】如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.
(1)求证:直线CP是⊙O的切线;
(2)若BC=2![]() ,sin∠BCP=
,sin∠BCP=![]() ,求⊙O的半径及△ACP的周长.
,求⊙O的半径及△ACP的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com