
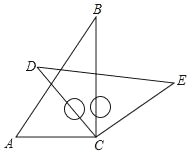
【题目】将一副三角板中的两块直角板中的两个直角顶点重合在一起,即按如图所示的方式叠放在一起,其中∠A=60°,∠B=30,∠D=45°.
(1)若∠BCD=45°,求∠ACE的度数.
(2)若∠ACE=150°,求∠BCD的度数.
(3)由(1)、(2)猜想∠ACE与∠BCD存在什么样的数量关系并说明理由.

【答案】(1)∠ACE=135°;(2)∠BCD=30°;(3)∠ACE与∠BCD互补.理由见解析.
【解析】
(1)先求得∠ACD的度数,即可得到∠ACE的度数;
(2)先求得∠ACD的度数,即可得到∠BCD的度数;
(3)依据∠BCD=∠ACB﹣∠ACD=90°﹣∠ACD,∠ACE=∠DCE+∠ACD=90°+∠ACD,即可得到∠ACE与∠BCD互补.
解:(1)∵∠BCD=45°,∠ACB=90°,
∴∠ACD=∠ACB﹣∠DCB=45°,
又∵∠DCE=90°,
∴∠ACE=∠ACD+∠DCE=45°+90°=135°;
(2)∵∠ACE=150°,∠DCE=90°,
∴∠ACD=∠ACE﹣∠DCE=150°﹣90°=60°,
又∵∠ACB=90°,
∴∠BCD=∠ACB﹣∠ACD=90°﹣60°=30°;
(3)由(1)、(2)猜想∠ACE与∠BCD互补.
理由:∵∠BCD=∠ACB﹣∠ACD=90°﹣∠ACD,
∠ACE=∠DCE+∠ACD=90°+∠ACD,
∴∠BCD+∠ACE=90°﹣∠ACD+90°+∠ACD=180°,
∴∠ACE与∠BCD互补.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】在直角坐标系中描出下列各组点,并将各组的点用线段依次连结起来.
(1)(1,0)、(6,0)、(6,1)、(5,0)、(6,-1)、(6,0);
(2)(2,0)、(5,3)、(4,0);
(3)(2,0)、(5,-3)、(4,0).
观察所得到的图形像什么?如果要将此图形向上平移到x轴上方,那么至少要向上平移几个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把2018个正整数1,2,3,4,…,2018按如图方式排列成一个表.

(1)用如图方式框住表中任意4个数,记左上角的一个数为![]() ,则另三个数用含
,则另三个数用含![]() 的式子表示出来,从小到大依次是__________、___________、_______________(请直接填写答案);
的式子表示出来,从小到大依次是__________、___________、_______________(请直接填写答案);
(2)用(1)中方式被框住的4个数之和可能等于2019吗?如果可能,请求出![]() 的值;如果不可能,请说明理由.
的值;如果不可能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成绩满分均为100分,然后再按笔试占60%、面试占40%计算候选人的综合成绩(满分为100分).
他们的各项成绩如下表所示:
修造人 | 笔试成绩/分 | 面试成绩/分 |
甲 | 90 | 88 |
乙 | 84 | 92 |
丙 | x | 90 |
丁 | 88 | 86 |
(1)直接写出这四名候选人面试成绩的中位数;
(2)现得知候选人丙的综合成绩为87.6分,求表中x的值;
(3)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市“健益”超市购进一批![]() 元/千克的绿色食品,如果以
元/千克的绿色食品,如果以![]() 元/千克销售,那么每天可售出
元/千克销售,那么每天可售出![]() 千克.由销售经验知,每天销售量
千克.由销售经验知,每天销售量![]() (千克)与销售单价
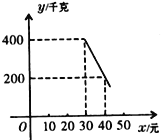
(千克)与销售单价![]() (元)(
(元)(![]() )存在如下图所示的一次函数关系.
)存在如下图所示的一次函数关系.
(1)试求出y与x的函数关系式;
(2)设“健益”超市销售该绿色食品每天获得利润p元,当销售单价为何值时,每天可获得 最大利润?最大利润是多少?
(3)根据市场调查,该绿色食品每天可获利润不超过4480元,现该超市经理要求每天利润不得低于4180元,请你帮助该超市确定绿色食品销售单价x的范围(直接写出).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC为⊙O的直径,CA是⊙O的切线,连接AB交⊙O于点D,连接CD,∠BAC的平分线交BC于点E,交CD于点F.
(1)求证:CE=CF;
(2)若BD=![]() DC,求
DC,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=BD,点E,F分别在BC,CD边上,且CE=DF,BF与DE交于点G,若BG=2,DG=4,则CD长为( )

A. ![]() B.
B. ![]() C. 6 D.
C. 6 D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com