
【题目】如图,BC为⊙O的直径,CA是⊙O的切线,连接AB交⊙O于点D,连接CD,∠BAC的平分线交BC于点E,交CD于点F.
(1)求证:CE=CF;
(2)若BD=![]() DC,求
DC,求![]() 的值.
的值.

【答案】(1)证明见解析(2)![]()
【解析】
(1)如下图,由已知易得∠ACB=∠BDC=∠ADC=90°,由此可得∠1+∠3=90°,∠2+∠5=90°结合∠1=∠2,可得∠3=∠5,结合∠3=∠4可得∠4=∠5,从而可得CE=CF;
(2)由(1)中所得∠1=∠2,∠3=∠5可得△ADF∽△ACE,由此可得![]() 由BD=
由BD=![]() DC,∠BDC=90°可得tan∠ABC=
DC,∠BDC=90°可得tan∠ABC=![]() ,再证∠ACD=∠ABC即可得到tan∠ACD=
,再证∠ACD=∠ABC即可得到tan∠ACD=![]() ,这样在Rt△ACD中,可得sin∠ACD=
,这样在Rt△ACD中,可得sin∠ACD=![]() ,由此即可得到
,由此即可得到![]() .
.
(1)∵BC为直径,
∴∠BDC=∠ADC=90°,
∴∠1+∠3=90° ,
∵AC是⊙O的切线,
∴∠ACB=90°,
∴∠2+∠5=90°,
∵AE平分∠BAC,
∴∠1=∠2,
∴∠3=∠5,
∵∠3=∠4
∴∠4=∠5,
∴ CF=CE ;
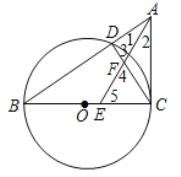
(2)由(1)可知∠1=∠2,∠3=∠5,
∴△ADF∽△ACE,
∴![]() ,
,
∵BD=![]() DC,∠BDC=90°,
DC,∠BDC=90°,
∴tan∠ABC=![]() ,
,
∵∠ABC+∠BAC=90°, ∠ACD+∠BAC=90°
∴∠ACD=∠ABC,
∴tan∠ACD=![]() ,
,
∴sin∠ACD=![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0 ②4a+2b+c>0 ③4ac﹣b2<8a ④![]() <a<
<a<![]() ⑤b>c.其中含所有正确结论的选项是( )
⑤b>c.其中含所有正确结论的选项是( )

A. ①③ B. ①③④ C. ②④⑤ D. ①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板中的两块直角板中的两个直角顶点重合在一起,即按如图所示的方式叠放在一起,其中∠A=60°,∠B=30,∠D=45°.
(1)若∠BCD=45°,求∠ACE的度数.
(2)若∠ACE=150°,求∠BCD的度数.
(3)由(1)、(2)猜想∠ACE与∠BCD存在什么样的数量关系并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
材料1、若一元二次方程ax2+bx+c=0(a≠0)的两根为x1,x2,则x1+x2=![]() ,x1x2=
,x1x2=![]() .
.
材料2、已知实数m、n满足m2﹣m﹣1=0,n2﹣n﹣1=0,且m≠n,求![]() 的值.
的值.
解:由题知m、n是方程x2﹣x﹣1=0的两个不相等的实数根,根据材料1得
m+n=1,mn=﹣1
∴![]()
根据上述材料解决下面问题;
(1)一元二次方程2x2+3x﹣1=0的两根为x1、x2,则x1+x2= ,x1x2= .
(2)已知实数m、n满足2m2﹣2m﹣1=0,2n2﹣2n﹣1=0,且m≠n,求m2n+mn2的值.
(3)已知实数p、q满足p2=3p+2,2q2=3q+1,且p≠2q,求p2+4q2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店开展优惠售书活动,一次购书定价不超过200元的打九折;一次购书定价超过200元的,其中200元按九折计算,超过200元的部分打八折.小丽挑选了几本喜爱的书,计算定价后,准备支付144元,遇见同学小芳也在买书,计算小芳购书的定价后,小丽对小芳说:我们独自付款,都只能享受九折,合在一-起付款,按今天的活动一共可优惠 48元.请根据以上内容解答下列问题:
(1)小丽购书的定价是____元 .
(2)列方程求解小芳购书的定价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,有一抛物线其表达式为![]() .
.
(1)当该抛物线过原点时,求![]() 的值;
的值;
(2)坐标系内有一矩形OABC,其中![]() 、
、![]() .
.
①直接写出C点坐标;
②如果抛物线![]() 与该矩形有2个交点,求
与该矩形有2个交点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上(与
上(与![]() 、
、![]() 不重合),四边形
不重合),四边形![]() 为正方形,过点
为正方形,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,对于下列结论:①
,对于下列结论:①![]() ;②四边形
;②四边形![]() 是矩形;③
是矩形;③![]() .其中正确的是( )
.其中正确的是( )

A.①②③B.①②C.①③D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小靓用七巧板拼成一幅装饰图,放入长方形ABCD内,装饰图中的三角形顶点E,F分别在边AB,BC上,三角形①的边GD在边AD上,若图1正方形中MN=1,则CD=____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com