
【题目】在平面直角坐标系xOy中,有一抛物线其表达式为![]() .
.
(1)当该抛物线过原点时,求![]() 的值;
的值;
(2)坐标系内有一矩形OABC,其中![]() 、
、![]() .
.
①直接写出C点坐标;
②如果抛物线![]() 与该矩形有2个交点,求
与该矩形有2个交点,求![]() 的取值范围.
的取值范围.
【答案】(1)m=0(2)①(0,2)②当![]() 或
或![]() 时,图象与矩形有2个交点
时,图象与矩形有2个交点
【解析】
(1)根据题意将原点的坐标(0,0)代入抛物线![]() 中,即可解得m的值;
中,即可解得m的值;
(2)①由已知条件结合矩形的性质可得OC=AB=2,由此可得点C的坐标为(0,2);
②由![]() 可知,抛物线的开口向上,顶点在x轴上;由此可知:当抛物线对称轴右侧的图象过点C时,抛物线与矩形只有1个交点,而当抛物线过原点是,抛物线和矩形有两个交点,即当抛物线对称轴右侧的图象过线段OC上的点(不包括点C)时,抛物线与矩形有两个交点;同理当抛物线对称轴左侧的图象过线段AB上的点(不包括点B)时,抛物线与矩形也有两个交点,这样结合已知条件即可求得对应的m的取值范围了.
可知,抛物线的开口向上,顶点在x轴上;由此可知:当抛物线对称轴右侧的图象过点C时,抛物线与矩形只有1个交点,而当抛物线过原点是,抛物线和矩形有两个交点,即当抛物线对称轴右侧的图象过线段OC上的点(不包括点C)时,抛物线与矩形有两个交点;同理当抛物线对称轴左侧的图象过线段AB上的点(不包括点B)时,抛物线与矩形也有两个交点,这样结合已知条件即可求得对应的m的取值范围了.
(1)∵ ![]() 的图象过原点,
的图象过原点,
∴![]() ,
,
解得![]() ;
;
(2)①∵点A、B的坐标分别为(4,0)和(4,2),
∴AB=2,
∵四边形OABC是矩形,
∴OC=2,
∴点C的坐标为(0,2);
②由于![]() ,
,
∴该函数图象开口向上,顶点在x轴上,
如下图所示:当对称轴右侧的图象过点![]() 时图象与矩形有1个交点,
时图象与矩形有1个交点,
此时:![]() ,解得
,解得![]() (舍去)或
(舍去)或![]() ,
,
当抛物线过原点时,抛物线与矩形有2个交点,
此时:由(1)可得![]() ,
,
∴当![]() ,时图象与矩形有2个交点;
,时图象与矩形有2个交点;
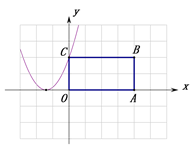
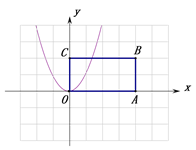
同理:当图象过点![]() 时解得
时解得![]() ,
,
当图象对称轴左侧部分过![]() 是,解得
是,解得![]() ,
,
∴当![]() 时,抛物线与矩形也有两个交点;
时,抛物线与矩形也有两个交点;
综上所述,当![]() 或
或![]() 时,抛物线与矩形有2个交点.
时,抛物线与矩形有2个交点.


科目:初中数学 来源: 题型:
【题目】某校八年级全体同学参加了某项捐款活动,随机抽查了部分同学捐款的情况统计如图所示
(1)本次共抽查学生____人,并将条形图补充完整;
(2)捐款金额的众数是_____,平均数是_____;
(3)在八年级700名学生中,捐款20元及以上(含20元)的学生估计有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下是通过折叠正方形纸片得到等边三角形的步骤取一张正方形的纸片进行折叠,具体操作过程如下:
第一步:如图,先把正方形ABCD对折,折痕为MN;
第二步:点E在线段MD上,将△ECD沿EC翻折,点D恰好落在MN上,记为点P,连接BP可得△BCP是等边三角形
问题:在折叠过程中,可以得到PB=PC;依据是________________________.
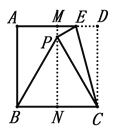
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC为⊙O的直径,CA是⊙O的切线,连接AB交⊙O于点D,连接CD,∠BAC的平分线交BC于点E,交CD于点F.
(1)求证:CE=CF;
(2)若BD=![]() DC,求
DC,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程ax2+bx﹣1=0(a≠0)有一根为x=2019,则一元二次方程a(x﹣1)2+b(x﹣1)=1必有一根为( )
A.![]() B.2020C.2019D.2018
B.2020C.2019D.2018
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市水果批发部门欲将A市的一批水果运往本市销售,有火车和汽车两种运输方式,运输过程中的损耗均为200元/时。其它主要参考数据如下:
运输工具 | 途中平均速度(千米/时) | 运费(元/千米) | 装卸费用(元) |
火车 | 100 | 15 | 2000 |
汽车 | 80 | 20 | 900 |
(1)如果汽车的总支出费用比火车费用多1100元,你知道本市与A市之间的路程是多少千米吗?请你列方程解答.
(2)如果A市与某市之间的距离为S千米,且知道火车与汽车在路上耽误的时间分别为2小时和3.1小时,你若是某市水果批发部门的经理,要将这种水果从A市运往本市销售。你将选择哪种运输方式比较合算呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D为BC中点,AE∥BD,且AE=BD.
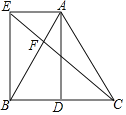
(1)求证:四边形AEBD是矩形;
(2)连接CE交AB于点F,若BE=2![]() ,AE=2,求EF的长.
,AE=2,求EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com