练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

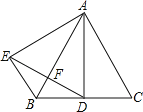
    【题目】如图，为正三角形，是的角平分线，也是正三角形，下列结论：①：②：③，其中正确的有________（填序号）.

    【答案】①②③

    【解析】

    由等边三角形的性质可得AE=AD，∠CAD=∠BAD=30°，AD⊥BC，可得∠BAE=∠BAD=30°，且AE=AD，可得EF=DF，“SAS”可证△ABE≌△ABD，可得BE=BD，即可求解．

    解：∵△ABC和△ADE是等边三角形，AD为∠BAC的角平分线，
    ∴AE=AD，∠CAD=∠BAD=30°，AD⊥BC，
    ∴∠BAE=∠BAD=30°，且AE=AD，
    ∴EF=DF
    ∵AE=AD，∠BAE=∠BAD，AB=AB
    ∴△ABE≌△ABD（SAS），
    ∴BE=BD
    ∴正确的有①②③
    故答案为：①②③

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，有一抛物线其表达式为.

    （1）当该抛物线过原点时，求的值；

    （2）坐标系内有一矩形OABC,其中、.

    ①直接写出C点坐标；

    ②如果抛物线与该矩形有2个交点，求的取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抛物线y=x2+bx+c的对称轴为直线x=1，该抛物线与x轴的两个交点分别为A和B，与y轴的交点为C，其中A（-1，0）.

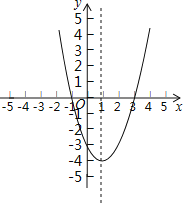
    （1）写出B点的坐标 ；

    （2）求抛物线的函数解析式；

    （3）若抛物线上存在一点P，使得△POC的面积是△BOC的面积的2倍，求点P的坐标；

    （4）点M是线段BC上一点，过点M作x轴的垂线交抛物线于点D，求线段MD长度的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】七年级一班和二班各推选名同学进行投篮比赛，按照比赛规则，每人各投了个球，两个班选手的进球数统计如下表，请根据表中数据回答问题．

    进球数（个）

    一班人数（人）

    二班人数（人）

    填表；

    平均数

    中位数

    众数

    方差

    一班

    2.6

    二班

    7

    7

    7

    如果要从这两个班中选出一个班代表级部参加学校的投篮比赛，争取夺得总进球数团体第一名，你认为应该选择哪个班？如果要争取个人进球数进入学校前三名，你认为应该选择哪个班？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若整数使关于的方程有负整数解，且也是四条直线在平面内交点的个数，则满足条件的所有的个数为（ ）

    A.3B.4C.5D.6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若关于的不等式组有三个整数解，且关于的分式方程有整数解，则满足条件的所有整数的和是（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，已知AB=AC=10cm，BC=16cm，AD⊥BC于D，点E、F分别从B、C两点同时出发，其中点E沿BC向终点C运动，速度为4cm/s；点F沿CA、AB向终点B运动，速度为5cm/s，设它们运动的时间为x（s）．

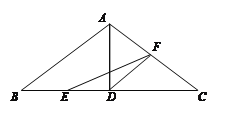
    （1）求x为何值时，△EFC和△ACD相似；

    （2）是否存在某一时刻，使得△EFD被 AD分得的两部分面积之比为3:5，若存在，求出x的值，若不存在，请说明理由；

    （3）若以EF为直径的圆与线段AC只有一个公共点，求出相应x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

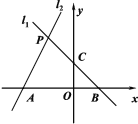
    【题目】如图，已知过点B（1，0）的直线与直线：相交于点P（－1，a）．且l1与y轴相交于C点，l2与x轴相交于A点．

    （1）求直线的解析式；

    （2）求四边形的面积；

    （3）若点Q是x轴上一动点，连接PQ、CQ，当△QPC周长最小时，求点Q坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知：∠BAC的平分线与BC的垂直平分线DG相交于点D，DE⊥AB，DF⊥AC，垂足分别为E、F，AB=6，AC=3，则BE=_____．

    查看答案和解析>>

    同步练习册答案