
【题目】如图,在菱形ABCD中,AB=BD,点E,F分别在BC,CD边上,且CE=DF,BF与DE交于点G,若BG=2,DG=4,则CD长为( )

A. ![]() B.
B. ![]() C. 6 D.
C. 6 D. ![]()
【答案】A
【解析】分析: 作辅助线,构建全等三角形,证明△DBE≌△BCF和△BGD≌△BHC,计算DE=BF=![]() ,再证明△BGE∽△BCF,列比例式得:
,再证明△BGE∽△BCF,列比例式得:![]() =
=![]() ,求得CF=±
,求得CF=±![]() ,从而得CD的长.
,从而得CD的长.
详解: 延长DE至H,使GH=BG,连接BH、CH,

∵四边形ABCD为菱形,
∴BC=DC=AB=BD,
∴△BDC是等边三角形,
∴∠DBC=∠BCF=60°,
∵CE=DF,
∴BC-CE=CD-DF,
即BE=CF,
在△DBE和△BCF中,
∵ ,
,
∴△DBE≌△BCF(SAS),
∴∠BDG=∠FBC,
∴∠BDG+∠DBF=∠FBC+∠DBF=60°,
∴∠BGE=∠BDG+∠DBF=60°,
∴△BGH为等边三角形,
∴BG=BH=2,∠GBH=60°,
∴∠DBF+∠FBC=∠HBC+∠FBC,
∴∠DBF=∠HBC,
在△BGD和△BHC中,
∵ ,
,
∴△BGD≌△BHC(SAS),
∴DG=CH=4,
∵∠FBC=∠BDG=∠BCH,
∴BF∥CH,
∴△BGE∽△CEH,
∴![]() ,
,
∵EG+EH=2,
∴EG=![]() ,
,
∴BF=DE=4+![]() =
=![]() ,
,
∵∠FBC=∠FBC,∠BGE=∠BCD=60°,
∴△BGE∽△BCF,
∴![]() ,
,
∴ ,
,
∴CF2=![]() ,
,
CF=±![]() ,
,
∴BE=CF=![]() ,
,
∴BC=3BE=3×![]() =2
=2![]() ,
,
∴CD=BC=2![]() .
.
故答案为:A.
点睛: 本题考查了菱形的性质、三角形全等的性质和判定、三角形相似的性质和判定、等边三角形的性质和判定,作辅助线,构建全等三角形是本题的关键,根据有一个角是60°的等腰三角形是等边三角形得△BGH为等边三角形是突破口.


科目:初中数学 来源: 题型:
【题目】将一副三角板中的两块直角板中的两个直角顶点重合在一起,即按如图所示的方式叠放在一起,其中∠A=60°,∠B=30,∠D=45°.
(1)若∠BCD=45°,求∠ACE的度数.
(2)若∠ACE=150°,求∠BCD的度数.
(3)由(1)、(2)猜想∠ACE与∠BCD存在什么样的数量关系并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上(与
上(与![]() 、
、![]() 不重合),四边形
不重合),四边形![]() 为正方形,过点
为正方形,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,对于下列结论:①
,对于下列结论:①![]() ;②四边形
;②四边形![]() 是矩形;③
是矩形;③![]() .其中正确的是( )
.其中正确的是( )

A.①②③B.①②C.①③D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小靓用七巧板拼成一幅装饰图,放入长方形ABCD内,装饰图中的三角形顶点E,F分别在边AB,BC上,三角形①的边GD在边AD上,若图1正方形中MN=1,则CD=____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、B、C、D、E在同一直线上,且AC=BD,E是线段BC的中点.
![]()
(1)点E是线段AD的中点吗?说明理由;
(2)当AD=10,AB=3时,求线段BE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=x2+bx+c的对称轴为直线x=1,该抛物线与x轴的两个交点分别为A和B,与y轴的交点为C,其中A(-1,0).
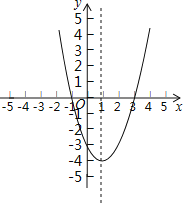
(1)写出B点的坐标 ;
(2)求抛物线的函数解析式;
(3)若抛物线上存在一点P,使得△POC的面积是△BOC的面积的2倍,求点P的坐标;
(4)点M是线段BC上一点,过点M作x轴的垂线交抛物线于点D,求线段MD长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学生利用暑假40天社会实践进行创业,他在网上开了一家微店,销售推广一种成本为25元/件的新型商品.在40天内,其销售单价n(元/件)与时间x(天)的关系式是:当1≤x≤20时,![]() ;当21≤x≤40时,
;当21≤x≤40时,![]() .这40天中的日销售量m(件)与时间x(天)符合函数关系,具体情况记录如下表(天数为整数):
.这40天中的日销售量m(件)与时间x(天)符合函数关系,具体情况记录如下表(天数为整数):
时间x(天) | 5 | 10 | 15 | 20 | 25 | … |
日销售量m(件) | 45 | 40 | 35 | 30 | 25 | … |
(1)请求出日销售量m(件)与时间x(天)之间的函数关系式;
(2)若设该同学微店日销售利润为w元,试写出日销售利润w(元)与时间x(天)的函数关系式;
(3)求这40天中该同学微店日销售利润不低于640元有多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com