
【题目】用适当的方法解下列方程![]()
(1)![]() (2)
(2)![]()
(3)![]() (4)
(4)![]()
(5)![]()
【答案】(1)x1=1,x2=-3;(2)x1=12,x2=-8;(3)![]() ,
,![]() ;(4)y1=-6,y2=
;(4)y1=-6,y2=![]() ;(5)x1=-2,x2=0.
;(5)x1=-2,x2=0.
【解析】
(1)移项、系数化为1,然后用直接开平方法求解即可;
(2)用配方法求解即可;
(3)用公式法求解即可;
(4)用直接开平方法求解即可;
(5)移项后,用因式分解法求解即可.
(1)∵![]() ,
,
∴![]() ,
,
∴x+1=±2,
∴x1=1,x2=-3;
(2)∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴x-2=±10,
∴x1=12,x2=-8;
(3)∵![]() ,
,
∴![]() ,
,
∵a=3,b=-4,c=-1,
∴=16+12=28>0,
∴![]() ,
,
∴ ![]() ,
,![]() ;
;
(4)∵![]() ,
,
∴![]() ,
,
∴3y=±(2y-6),
∴3y=2y-6,3y=-2y+6,
∴y1=-6,y2=![]() ;
;
(5)∵![]() ,
,
∴![]() ,
,
∴(x+2)(x+2-2)=0,
∴x+2=0,x+2-2=0,
∴x1=-2,x2=0.


科目:初中数学 来源: 题型:
【题目】某市“健益”超市购进一批![]() 元/千克的绿色食品,如果以
元/千克的绿色食品,如果以![]() 元/千克销售,那么每天可售出
元/千克销售,那么每天可售出![]() 千克.由销售经验知,每天销售量
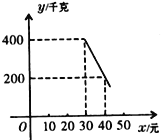
千克.由销售经验知,每天销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元)(
(元)(![]() )存在如下图所示的一次函数关系.
)存在如下图所示的一次函数关系.
(1)试求出y与x的函数关系式;
(2)设“健益”超市销售该绿色食品每天获得利润p元,当销售单价为何值时,每天可获得 最大利润?最大利润是多少?
(3)根据市场调查,该绿色食品每天可获利润不超过4480元,现该超市经理要求每天利润不得低于4180元,请你帮助该超市确定绿色食品销售单价x的范围(直接写出).
查看答案和解析>>
科目:初中数学 来源: 题型:
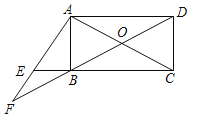
【题目】如图,平行四边形ABCD的对角线AC、BD交于点O,点E在边CB的延长线上,且∠EAC=90°,AE2=EBEC.
(1)求证:四边形ABCD是矩形;
(2)延长DB、AE交于点F,若AF=AC,求证:AE=BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=BD,点E,F分别在BC,CD边上,且CE=DF,BF与DE交于点G,若BG=2,DG=4,则CD长为( )

A. ![]() B.
B. ![]() C. 6 D.
C. 6 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
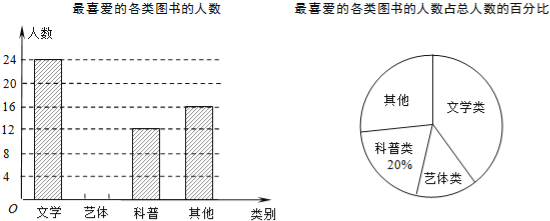
【题目】某校为了开阔学生的视野,积极组织学生参加课外读书活动.“放飞梦想”读书小组协助老师随机抽取本校的部分学生,调查他们最喜爱的图书类别(图书分为文学类、艺体类、科普类、其他等四类),并将调查结果绘制成如下两幅不完整的统计图,请你结合图中的信息解答下列问题:
(1)求被调查的学生人数;
(2)补全条形统计图;
(3)已知该校有1200名学生,估计全校最喜爱文学类图书的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个点从数轴上的原点开始,先向右移动1个单位长度,再向左移动2个单位长度,再向右移动3个单位长度,再向左移动4个单位长度,……,移动2019次后,该点所对应的数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由几个相同的边长为1的小立方块搭成的几何体的俯视图如下图,格中的数字表示该位置的小立方块的个数.
(1)请在下面方格纸中分别画出这个向何体的主视图和左视图.
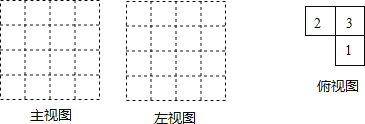
(2)根据三视图;这个组合几何体的表面积为 _________ 个平方单位.(包括底面积)
(3)若上述小立方块搭成的几何体的俯视图不变,各位置的小立方块个数可以改变(总数目不变),则搭成这样的组合几何体中的表面积最大是为 _________ 个平方单位.(包括底面积)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2-8ax(a<0)的图像与x轴的正半轴交于点A,它的顶点为P.点C为y轴正半轴上一点,直线AC与该图像的另一交点为B,与过点P且垂直于x轴的直线交于点D,且CB:AB=1:7.
(1)求点A的坐标及点C的坐标(用含a的代数式表示);
(2)连接BP,若△BDP与△AOC相似(点O为原点),求此二次函数的关系式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com