
【题目】某大学生利用暑假40天社会实践进行创业,他在网上开了一家微店,销售推广一种成本为25元/件的新型商品.在40天内,其销售单价n(元/件)与时间x(天)的关系式是:当1≤x≤20时,![]() ;当21≤x≤40时,
;当21≤x≤40时,![]() .这40天中的日销售量m(件)与时间x(天)符合函数关系,具体情况记录如下表(天数为整数):
.这40天中的日销售量m(件)与时间x(天)符合函数关系,具体情况记录如下表(天数为整数):
时间x(天) | 5 | 10 | 15 | 20 | 25 | … |
日销售量m(件) | 45 | 40 | 35 | 30 | 25 | … |
(1)请求出日销售量m(件)与时间x(天)之间的函数关系式;
(2)若设该同学微店日销售利润为w元,试写出日销售利润w(元)与时间x(天)的函数关系式;
(3)求这40天中该同学微店日销售利润不低于640元有多少天?
【答案】(1)m=-x+50;(2)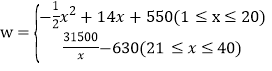 ;(3)这40天中该同学微店日销售利润不低于640元有13天.
;(3)这40天中该同学微店日销售利润不低于640元有13天.
【解析】(1)、首先设日销售量m(件)与时间x(天)之间的函数关系式为m=kx+b,然后利用待定系数法求出函数解析式;(2)、根据1≤x≤20和21≤x≤40两种情况分别求出w与x的函数关系式;(3)、分两段函数分别求出x的值,然后得出不等式,从而求出天数.
(1)、设日销售量m(件)与时间x(天)之间的函数关系式为m=kx+b,
把x=5,m=45代入得5k+b=45①, 把x=10,m=40代入得10k+b=40②,
将①②联立方程组解得![]() , ∴m=-x+50,
, ∴m=-x+50,
当x=15时m=35,当x=20时m=30,当x=25时m=25,
因此,经验证日销售量m(件)与时间x(天)之间的函数关系式为m=-x+50;
(2)、当1≤x≤20时,w=![]() =
=![]() =
=![]() ,
,
当21≤x≤40时,w=![]() =
=![]() =
=![]() ,
,
∴w关于x的函数关系式为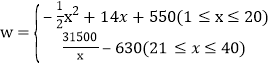 ;
;
(3)、当w=640时,![]() ∴
∴![]() ,解得x1=10,x2=18,
,解得x1=10,x2=18,
∴当1≤x≤20时,日利润不低于640元有:18-10+1=9(天).
若![]() 时,则x≈24.8
时,则x≈24.8
∴当21≤x≤40时,日利润不低于640元有:24-21+1=4(天), ∴9+4=13(天)
∴这40天中该同学微店日销售利润不低于640元有13天.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=BD,点E,F分别在BC,CD边上,且CE=DF,BF与DE交于点G,若BG=2,DG=4,则CD长为( )

A. ![]() B.
B. ![]() C. 6 D.
C. 6 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2-8ax(a<0)的图像与x轴的正半轴交于点A,它的顶点为P.点C为y轴正半轴上一点,直线AC与该图像的另一交点为B,与过点P且垂直于x轴的直线交于点D,且CB:AB=1:7.
(1)求点A的坐标及点C的坐标(用含a的代数式表示);
(2)连接BP,若△BDP与△AOC相似(点O为原点),求此二次函数的关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解学生孝敬父母的情况(选项:A为父母洗一次脚;B帮父母做一次家务;C给父母买一件礼物;D其它),在全校范围内随机抽取了若干名学生进行调查,得到如下图表(部分信息未给出):
根据以上信息解答下列问题:


(1)这次被调查的学生有多少人?
(2)求表中m,n,p的值,并补全条形统计图.
(3)该校有1600名学生,估计该校全体学生中选择B选项的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两直线L1:y=k1x+b1,L2:y=k2x+b2,若L1⊥L2,则有k1k2=﹣1.
(1)应用:已知y=2x+1与y=kx﹣1垂直,求k;
(2)直线经过A(2,3),且与y=![]() x+3垂直,求解析式.
x+3垂直,求解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 为坐标原点,正方形
为坐标原点,正方形![]() 与长方形
与长方形![]() 的位置如图所示,点
的位置如图所示,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() ,
,![]() 在
在![]() 轴的负半轴上(点
轴的负半轴上(点![]() 在点
在点![]() 的右侧),点
的右侧),点![]() 的坐标为
的坐标为![]() ,
,![]() ,实数
,实数![]() ,
,![]() 的值满足
的值满足![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)长方形![]() 以每秒1个单位长度的速度向右平移
以每秒1个单位长度的速度向右平移![]() (
(![]() )秒得到矩形
)秒得到矩形![]() ,点
,点![]() ,
,![]() ,
,![]() ,
,![]() 分别为点
分别为点![]() ,
,![]() ,
,![]() ,
,![]() 平移后的对应点,设矩形
平移后的对应点,设矩形![]() 与正方形
与正方形![]() 重合部分的面积为
重合部分的面积为![]() ,用含
,用含![]() 的式子表示
的式子表示![]() ,并直接写出相应的
,并直接写出相应的![]() 的范围;
的范围;
(3)在(2)的条件下,在长方形![]() 出发运动的同时,点
出发运动的同时,点![]() 从点
从点![]() 出发,沿正方形的边以每秒2个单位长度的速度顺时针方向运动(即
出发,沿正方形的边以每秒2个单位长度的速度顺时针方向运动(即![]() ),连接
),连接![]() ,
,![]() ,当三角形
,当三角形![]() 的面积为15时,求
的面积为15时,求![]() 时相应的
时相应的![]() 值,并直接写出此时刻
值,并直接写出此时刻![]() 值及点
值及点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
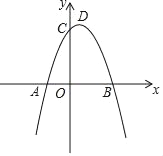
【题目】如图,已知抛物线y=ax2+2x+8与x轴交于A,B两点,与y轴交于点C,且B(4,0).
(1)求抛物线的解析式及其顶点D的坐标;
(2)如果点P(p,0)是x轴上的一个动点,则当|PC﹣PD|取得最大值时,求p的值;
(3)能否在抛物线第一象限的图象上找到一点Q,使△QBC的面积最大,若能,请求出点Q的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(方法回顾)证明:三角形中位线定理.
已知:如图1,![]() 中,D、E分别是AB、AC的中点.
中,D、E分别是AB、AC的中点.
求证:![]() ,
,![]() .
.
证明:如图1,延长DE到点F,使得![]() ,连接CF;
,连接CF;
请继续完成证明过程;

(2)(问题解决)
如图2,在矩形ABCD中,E为AD的中点,G、F分别为AB、CD边上的点,若![]() ,
,![]() ,
,![]() ,求GF的长.
,求GF的长.
(3)(思维拓展)
如图3,在梯形ABCD中,![]() ,
,![]() ,
,![]() ,E为AD的中点,G、F分别为AB、CD边上的点,若
,E为AD的中点,G、F分别为AB、CD边上的点,若![]() ,
,![]() ,
,![]() ,求GF的长.
,求GF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com