
【题目】探究题:如图,AB⊥BC,射线CM⊥BC,且BC=5cm,AB=1cm,点P是线段BC(不与点B、C重合)上的动点,过点P作DP⊥AP交射线CM于点D,连结AD.

(1)如图1,若BP=4cm,则CD= ;
(2)如图2,若DP平分∠ADC,试猜测PB和PC的数量关系,并说明理由;
(3)若△PDC是等腰三角形,则CD= cm.(请直接写出答案)
【答案】(1)4cm;(2)PB=PC,理由见解析;(3)4
【解析】
(1)根据AAS定理证明△ABP≌△PCD,可得BP=CD;
(2)延长线段AP、DC交于点E,分别证明△DPA≌△DPE、△APB≌△EPC,根据全等三角形的性质解答;
(3)根据等腰直角三角形的性质计算.
解:(1)∵BC=5cm,BP=4cm,
∴PC=1cm,
∴AB=PC,
∵DP⊥AP,
∴∠APD=90°,
∴∠APB+∠CPD=90°,
∵∠APB+∠CPD=90°,∠APB+∠BAP=90°,
∴∠BAP=∠CPD,
在△ABP和△PCD中,
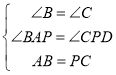 ,
,
∴△ABP≌△PCD,
∴BP=CD=4cm;
(2)PB=PC,
理由:如图2,延长线段AP、DC交于点E,
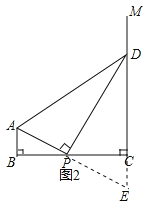
∵DP平分∠ADC,
∴∠ADP=∠EDP.
∵DP⊥AP,
∴∠DPA=∠DPE=90°,
在△DPA和△DPE中,
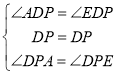 ,
,
∴△DPA≌△DPE(ASA),
∴PA=PE.
∵AB⊥BP,CM⊥CP,
∴∠ABP=∠ECP=Rt∠.
在△APB和△EPC中,
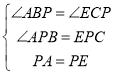 ,
,
∴△APB≌△EPC(AAS),
∴PB=PC;
(3)∵△PDC是等腰三角形,
∴△PCD为等腰直角三角形,即∠DPC=45°,
又∵DP⊥AP,
∴∠APB=45°,
∴BP=AB=1cm,
∴PC=BC﹣BP=4cm,
∴CD=CP=4cm,
故答案为:4.


 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有若干个白球和红球,这些球除颜色外都相同,某课外学习小组做摸球试验,将求搅均匀后从张任意摸出一个球,记下颜色后放回,搅匀,不断重复,获得数据如下
摸球次数 |
|
|
|
|
|
|
摸到白球的频数 |
|
|
|
|
|
|
摸到白球的频率 |
![]() 计算并填写表中摸到白球的频率;
计算并填写表中摸到白球的频率;
![]() 当摸球次数很大时,摸到的白球的频率估计值是多少?
当摸球次数很大时,摸到的白球的频率估计值是多少?
![]() 若已知袋中有白球
若已知袋中有白球![]() 个,试估计袋中红球的个数.
个,试估计袋中红球的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在大课间活动中,同学们积极参加体育锻炼,小明就本班同学“我最喜爱的体育项目”进行了一次调查统计,下面是他通过收集数据后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:
(1)该班共有_____名学生;
(2)补全条形统计图;
(3)在扇形统计图中,“乒乓球”部分所对应的圆心角度数为_____;
(4)学校将举办体育节,该班将推选5位同学参加乒乓球活动,有3位男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学组成双打组合,用树状图或列表法求恰好选出一男一女组成混合双打组合的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,AD=5,E为BC上一点,BE∶CE=3∶2,连接AE,点P从点A出发,沿射线AB的方向以每秒1个单位长度的速度匀速运动,过点P作PF∥BC交直线AE于点F.
(1)线段AE=______;
(2)设点P的运动时间为t(s),EF的长度为y,求y关于t的函数关系式,并写出t的取值范围;
(3)当t为何值时,以F为圆心的⊙F恰好与直线AB、BC都相切?并求此时⊙F的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC∽△ADE,AE=5cm,EC=3cm,BC=7cm,∠BAC=45°,∠C=40°.

(1)求∠AED和∠ADE的大小;
(2)求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
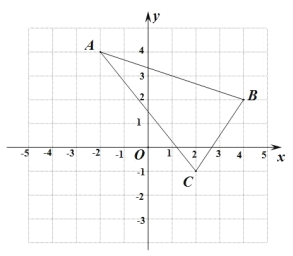
【题目】如图,△ABC 在平面直角坐标系中,点 A,B,C 的坐标分别为 A(-2,4),B(4,2),C(2,-1).
(Ⅰ)请在平面直角坐标系内,画出△ABC 关于 x 轴的对称图形△A1B1C1,其中,点 A,B,C 的对应点分别为A1,B1,C1;
(Ⅱ)请写出点C(2,-1)关于直线m(直线m上格点的横坐标都为-1)对称的点C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
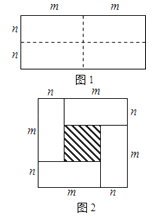
【题目】图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)请写出图2中阴影部分的面积;
(2)观察图2你能写出下列三个代数式之间的等量关系吗?
代数式:(m+n)2, (m﹣n)2, mn;
(3)根据(2)中的等量关系,解决如下问题:若a+b=7,ab=5,求(a﹣b)2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,抛物线![]() 经过点
经过点![]() 、
、![]() .
.
![]() 求
求![]() 、
、![]() 的值;
的值;
![]() 如图,点
如图,点![]() 与点
与点![]() 关于点
关于点![]() 对称,过点
对称,过点![]() 的直线交
的直线交![]() 轴于点
轴于点![]() ,交抛物线于另一点
,交抛物线于另一点![]() .若
.若![]() ,求
,求![]() 的值;
的值;
![]() 如图,在
如图,在![]() 的条件下,点
的条件下,点![]() 是
是![]() 轴上一点,连
轴上一点,连![]() 、
、![]() 分别交抛物线于点
分别交抛物线于点![]() 、
、![]() ,探究
,探究![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC 中,∠A=30°,∠B=90°,AC=8,点 D 在边 AB, 且 BD=![]() ,点 P 是△ABC 边上的一个动点,若 AP=2PD 时,则 PD的长是____________.
,点 P 是△ABC 边上的一个动点,若 AP=2PD 时,则 PD的长是____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com