
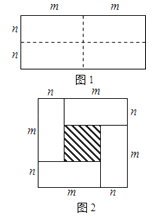
【题目】图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)请写出图2中阴影部分的面积;
(2)观察图2你能写出下列三个代数式之间的等量关系吗?
代数式:(m+n)2, (m﹣n)2, mn;
(3)根据(2)中的等量关系,解决如下问题:若a+b=7,ab=5,求(a﹣b)2的值.
科目:初中数学 来源: 题型:
【题目】探究题:如图,AB⊥BC,射线CM⊥BC,且BC=5cm,AB=1cm,点P是线段BC(不与点B、C重合)上的动点,过点P作DP⊥AP交射线CM于点D,连结AD.

(1)如图1,若BP=4cm,则CD= ;
(2)如图2,若DP平分∠ADC,试猜测PB和PC的数量关系,并说明理由;
(3)若△PDC是等腰三角形,则CD= cm.(请直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bc+c的图象如图所示,则下列判断中错误的是( )

A. 图象的对称轴是直线x=﹣1 B. 当x>﹣1时,y随x的增大而减小
C. 当﹣3<x<1时,y<0 D. 一元二次方程ax2+bx+c=0的两个根是﹣3,1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某茶叶公司经销一种茶叶,每千克成本为![]() 元,市场调查发现在一段时间内,销量
元,市场调查发现在一段时间内,销量![]() (千克)随销售单价
(千克)随销售单价![]() (元/千克)的变化而变化,具有关系为:
(元/千克)的变化而变化,具有关系为:![]() ,物价部门规定每千克的利润不得超过
,物价部门规定每千克的利润不得超过![]() 元.设这种茶叶在这段时间内的销售利润
元.设这种茶叶在这段时间内的销售利润![]() (元),解答下列问题:
(元),解答下列问题:
![]() 求
求![]() 与
与![]() 的关系式;
的关系式;
![]() 当
当![]() 取何值时,
取何值时,![]() 的值最大?并求出最大值;
的值最大?并求出最大值;
![]() 当销售利润
当销售利润![]() 的值最大时,销售额也是最大吗?判断并说明理由.
的值最大时,销售额也是最大吗?判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个关于![]() 的代数式
的代数式![]() ,若存在一个系数为正数关于
,若存在一个系数为正数关于![]() 的单项式
的单项式![]() ,使
,使![]() 的结果是所有系数均为整数的整式,则称单项式
的结果是所有系数均为整数的整式,则称单项式![]() 为代数式
为代数式![]() 的“整系单项式” ,例如:
的“整系单项式” ,例如:
当![]() 时,由于
时,由于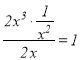 ,故
,故![]() 是
是![]() 的整系单项式;
的整系单项式;
当![]() 时,由于
时,由于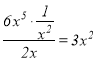 ,故
,故![]() 是
是![]() 的整系单项式;
的整系单项式;
当![]() 时,由于
时,由于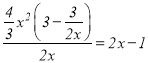 ,故
,故![]() 是
是![]() 的整系单项式;
的整系单项式;
当![]() 时,由于
时,由于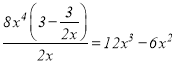 ,故
,故![]() 是
是![]() 的整系单项式;
的整系单项式;
显然,当代数式![]() 存在整系单项式
存在整系单项式![]() 时,
时,![]() 有无数个,现把次数最低,系数最小的整系单项式
有无数个,现把次数最低,系数最小的整系单项式![]() 记为
记为![]() ,例如:
,例如:![]() .
.
阅读以上材料并解决下列问题:
⑴.判断:当![]() 时,
时,![]()
![]() 的整系单项式(填“是”或“不是”);
的整系单项式(填“是”或“不是”);
⑵.当![]() 时,
时,![]() = ;
= ;
⑶.解方程: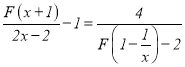 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠ABC=∠DCB,添加一个条件使△ABC≌△DCB,下列添加的条件不能使△ABC≌△DCB的是( )

A. ∠A=∠D B. AB=DC C. AC=DB D. OB=OC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com